
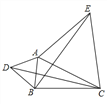
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() 分别交
分别交![]() 延长线于点
延长线于点![]() .
.
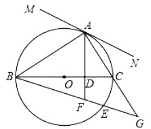
(1)过点![]() 作直线
作直线![]() ,使得
,使得![]() ,判断直线
,判断直线![]() 与
与![]() 的位置关系,并说理.
的位置关系,并说理.
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
(3)连接![]() ,探索线段
,探索线段![]() 与
与![]() 间的数量关系,并说明理由.
间的数量关系,并说明理由.
【答案】(1)直线![]() 与
与![]() 相切,理由详见解析;(2)
相切,理由详见解析;(2)![]() ;(3)
;(3)![]() ,证明详见解析.
,证明详见解析.
【解析】
(1)连接OA,根据![]() 得到
得到![]() ,由BC是
,由BC是![]() 直径,
直径,![]() ,得到
,得到![]() ,推出
,推出![]() ,利用
,利用![]() 得到
得到![]() ,推出
,推出![]() ,即可得到直线
,即可得到直线![]() 与
与![]() 相切的结论;
相切的结论;
(2)过点A作AM⊥BG于M,根据![]() 得到∠ACB=∠ABE,证得△AMB∽△BAC,得到
得到∠ACB=∠ABE,证得△AMB∽△BAC,得到![]() ,利用勾股定理求出BC=5,即可求出
,利用勾股定理求出BC=5,即可求出![]() ,再证明△ABM∽△GBA,求出BG=
,再证明△ABM∽△GBA,求出BG=![]() ;
;
(3)在![]() 上截取
上截取![]() ,连接
,连接![]() .证明
.证明![]() ,得到
,得到![]() ,由
,由![]() 得到
得到![]() ,推出
,推出![]() .
.
(1)解:直线![]() 与
与![]() 相切,
相切,
理由:连接OA,
∵![]() ,
,
∴![]() ,
,
∵BC是![]() 直径,
直径,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴直线![]() 与
与![]() 相切.
相切.

(2)过点A作AM⊥BG于M,
∵![]() ,
,
∴∠ACB=∠ABE,
∵∠BAC=∠AMB=90°,
∴△AMB∽△BAC,
∴![]() ,
,
∵∠BAC=90°,![]() ,
,![]() ,
,
∴BC=5,
∴![]() ,
,
∴![]() ,
,
∵∠BAC=∠AMB=90°,∠ABM=∠GBA,
∴△ABM∽△GBA,
∴![]() ,
,
∴![]() ,
,
∴BG=![]() ;
;

(3)![]() .
.
理由:在![]() 上截取
上截取![]() ,连接
,连接![]() .
.
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
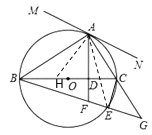
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=4,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
A.![]() B.
B.![]() C.
C.![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
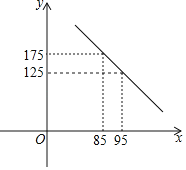
【题目】武汉“新冠肺炎”发生以来,某医疗公司积极复工,加班加点生产医用防护服,为防控一线助力.以下是该公司以往的市场调查,发现该公司防护服的日销售量y(套)与销售单价x(元)之间满足一次函数关系,如下图所示,关于日销售利润w(元)和销售单价x(元)的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 |
日销售利润w(元) | 875 | 1875 | 1875 |
(注:日销售利润=日销售量×(销售单价一成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围);
(2)根据函数图象和表格所提供的信息,填空:
该公司生产的防护服的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)该公司复工以后,在政府部门的帮助下,原材料采购成本比以往有了下降,平均起来,每生产一套防护服,成本比以前下降5元.该公司计划开展科技创新,以降低该产品的成本,如果在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的 1.5 倍,两人各加工 600 个这种零件,甲比乙少用 5 天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元,现有 3000 个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过 7800 元,那么甲至少加工了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点p为边AB上的一点,![]() CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
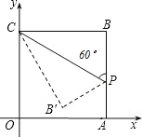
A.(2, 2![]() )B.(
)B.(![]() , 2-2
, 2-2![]() )C.(2, 4-2
)C.(2, 4-2![]() )D.(
)D.(![]() , 4-2
, 4-2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于A,B两点,交y轴于点C.直线
交x轴于A,B两点,交y轴于点C.直线![]() 经过点A,C.
经过点A,C.
(1)求抛物线的解析式;
(2)点P是抛物线上一动点,过点P作x轴的垂线,交直线AC于点M,设点P的横坐标为m.
①当![]() 是直角三角形时,求点P的坐标;
是直角三角形时,求点P的坐标;
②作点B关于点C的对称点![]() ,则平面内存在直线l,使点M,B,
,则平面内存在直线l,使点M,B,![]() 到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线
到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线![]() 的解析式.(k,b可用含m的式子表示)
的解析式.(k,b可用含m的式子表示)
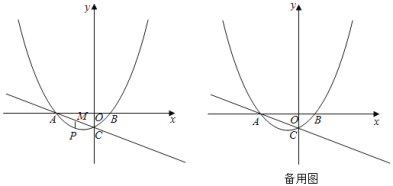
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE分别是以BC,DE为底边且顶角相等的等腰三角形,点D在线段BC上,AF平分DE交BC于点F,连接BE,EF.
(1)CD与BE相等?若相等,请证明;若不相等,请说明理由;
(2)若∠BAC=90°,求证:BF2+CD2=FD2.
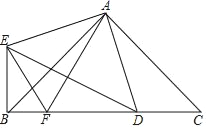
查看答案和解析>>
科目:初中数学 来源: 题型:
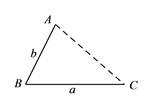
【题目】(1)发现
如图,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() .
.
填空:当点![]() 位于____________时,线段
位于____________时,线段![]() 的长取得最大值,且最大值为_________.(用含
的长取得最大值,且最大值为_________.(用含![]() ,
,![]() 的式子表示)
的式子表示)
(2)应用
点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() .如图所示,分别以
.如图所示,分别以![]() ,
,![]() 为边,作等边三角形
为边,作等边三角形![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() ,
,![]() .
.
①找出图中与![]() 相等的线段,并说明理由;
相等的线段,并说明理由;
②直接写出线段![]() 长的最大值.
长的最大值.
(3)拓展
如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 长的最大值及此时点
长的最大值及此时点![]() 的坐标.
的坐标.
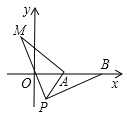
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com