
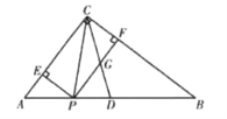
【题目】如图,在![]() 中,
中,![]() 为斜边
为斜边![]() 中点,点P从A出发,沿
中点,点P从A出发,沿![]() 以每秒5个单位的速度向终点B运动,过点P作
以每秒5个单位的速度向终点B运动,过点P作![]() 于F,得到矩形
于F,得到矩形![]() 与矩形
与矩形![]() 的一边交于点G,连接PC,设点P的运动时间为
的一边交于点G,连接PC,设点P的运动时间为![]() 秒.
秒.
(1)求线段![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)当![]() 时,求线段
时,求线段![]() 多长;
多长;
(3)当点P不与![]() 重合时,设矩形
重合时,设矩形![]() 与三角形CPD重叠部分图形的面积是
与三角形CPD重叠部分图形的面积是![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)在点P出发的同时,点Q从点D出发,沿![]() 以每秒6个单位的速度向终点D移动,当点Q在矩形
以每秒6个单位的速度向终点D移动,当点Q在矩形![]() 内部时,直接写出
内部时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)3;(3)
;(2)3;(3) ;(4)当
;(4)当![]() 时,且
时,且![]()
【解析】
(1)根据矩形的性质CF=EP,在三角形AEP中,利用三角函数比表示出EP即可;
(2))当![]() 时,求出AP和PD的长度,再证
时,求出AP和PD的长度,再证![]() ,利用相似比可得出PG的长度;
,利用相似比可得出PG的长度;
(3)分类讨论,当P点在AD上运动时或当P点在BD上运动时,通过相似三角形,用t的代数式表示出三角形CPG的面积即可;
(4)取几个极限位置点,Q点在PE和在PF上,及与C点重合的时候,算出t的值,综合起来确定t的取值范围即可;
(1)如图1,在三角形ABC中,![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
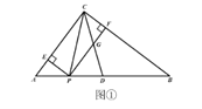
(2)如图1,当![]() 时,
时, ![]()
![]()
因为四边形PECF是矩形
所以![]()
![]()
![]()
(3)当P点在AD上运动时,即![]() 时,如图②可得:
时,如图②可得:
![]() ,
,![]()
![]()
当P点在DB上运动时,即![]() 时,如图③可得:
时,如图③可得:
![]() ,
,![]()
![]()
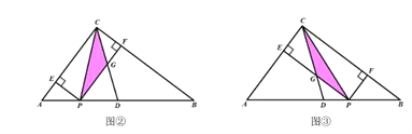
(4)
当点Q落在PF上时,如图④,有![]() ;
;
当点Q与点C重合时,![]() ;
;
当点Q落在PE上时,如图⑤时,![]() ,
,
综上可得,t的取值范围是:![]() ,且
,且![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确的有( )
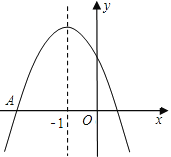
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-2mx+m2+m-1(m是常数).
(1)求证:不论m为何值,该函数的图像的顶点都在函数y=x-1的图像上.
(2)若该函数的图像与函数y=x+b的图像有两个交点,则b的取值范围为( )
A.b>0 B.b>-1 C.b>-![]() D.b>-2
D.b>-2
(3)该函数图像与坐标轴交点的个数随m的值变化而变化,直接写出交点个数及对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店欲购进![]() 两种商品,已知购进
两种商品,已知购进![]() 种商品5件和
种商品5件和![]() 种商品4件共需300元;若购进
种商品4件共需300元;若购进![]() 种商品6件和
种商品6件和![]() 种商品8件共需440元;
种商品8件共需440元;
(1)求![]() 两种商品每件的进价分别为多少元?
两种商品每件的进价分别为多少元?
(2)若该商店,![]() 种商品每件的售价为48元,
种商品每件的售价为48元,![]() 种商品每件的售价为31元,且商店将购进
种商品每件的售价为31元,且商店将购进![]() 共50件的商品全部售出后,要获得的利润超过348元,求
共50件的商品全部售出后,要获得的利润超过348元,求![]() 种商品至少购进多少件?
种商品至少购进多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
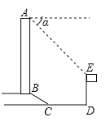
【题目】如图,某办公大楼正前方有一根高度是15米的旗杆![]() ,从办公大楼顶端
,从办公大楼顶端![]() 测得旗杆顶端
测得旗杆顶端![]() 的俯角
的俯角![]() 是45°,旗杆底端
是45°,旗杆底端![]() 到大楼前梯坎底边的距离
到大楼前梯坎底边的距离![]() 是10米,梯坎坡长
是10米,梯坎坡长![]() 是10米,梯坎坡度
是10米,梯坎坡度![]() =1:
=1:![]() ,则大楼
,则大楼![]() 的高为______米.
的高为______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生利用业余时间参与了一家网店经营,销售一种成本为30元/件的文化衫,根据以往的销售经验,他整理出这种文化衫的售价y1(元/件),销量y2(件)与第x(1≤x<90)天的函数图象如图所示(销售利润=(售价-成本)×销量).
(1)求y1与y2的函数解析式.
(2)求每天的销售利润W与x的函数解析式.
(3)销售这种文化衫的第多少天,销售利润最大,最大利润是多少?


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com