此题答案不唯一:如①AB=CD;②AC
2=AB•BC;③AD
2=BD.AB④CD
2=AC•AD;⑤AB
2=AD•AC;⑥CD
2=BC•BD等
分析:由AD是Rt△ABC的斜边BC上的高线,即可得S
△ABC=

AB•AC=

BC•AD,S
△ABD=

AD•BD,S
△ACD=

AD•CD,然后由要使△ACD的面积是△ABC和△ABD面积的比例中项,根据比例中项的性质,即可求得答案.
解答:∵AD是Rt△ABC的斜边BC上的高线,
∴S
△ABC=

AB•AC=

BC•AD,S
△ABD=

AD•BD,S
△ACD=

AD•CD,
∵要使△ACD的面积是△ABC和△ABD面积的比例中项,
即S
△ACD2=S
△ABC•S
△ABD,
∴(AD•CD)
2=AD•BC•AD•BD,
∴⑥CD
2=BC•BD;
∵AB
2=BC•BD,
∴①AB=CD;
∵AD
2=BD•CD,AC
2=BC•CD,
∴③AD
2=BD•AB,②AC
2=AB•BC;
∵(AD•CD)
2=AB•AC•AD•BD,AD
2=BD•AB,
∴④CD
2=AC•AD;
∴⑤AB
2=AD•AC;
有多种答案,如①AB=CD;②AC
2=AB•BC;③AD
2=BD•AB④CD
2=AC•AD;⑤AB
2=AD•AC;⑥CD
2=BC•BD等等.
故答案为:①AB=CD;②AC
2=AB•BC;③AD
2=BD.AB④CD
2=AC•AD;⑤AB
2=AD•AC;⑥CD
2=BC•BD.
点评:此题考查了直角三角形面积的求解方法与比例中项的性质.此题难度不大,解题的关键是注意掌握数形结合思想的应用与比例变形.

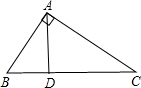 如图,AD是Rt△ABC的斜边BC上的高线,要使△ACD的面积是△ABC和△ABD面积的比例中项,请你添加一个适当的条件:________.
如图,AD是Rt△ABC的斜边BC上的高线,要使△ACD的面积是△ABC和△ABD面积的比例中项,请你添加一个适当的条件:________. AB•AC=
AB•AC= BC•AD,S△ABD=
BC•AD,S△ABD= AD•BD,S△ACD=
AD•BD,S△ACD= AD•CD,然后由要使△ACD的面积是△ABC和△ABD面积的比例中项,根据比例中项的性质,即可求得答案.
AD•CD,然后由要使△ACD的面积是△ABC和△ABD面积的比例中项,根据比例中项的性质,即可求得答案. AB•AC=
AB•AC= BC•AD,S△ABD=
BC•AD,S△ABD= AD•BD,S△ACD=
AD•BD,S△ACD= AD•CD,
AD•CD,

 名校课堂系列答案
名校课堂系列答案