
ЁОЬтФПЁПШчЭМЃЌвбжЊЪ§жсЩЯЕу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ,Еу
,Еу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ,вд
,вд![]() ЮЊБпдкЪ§жсЕФЩЯЗНзїе§ЗНаЮABCD.ЖЏЕу
ЮЊБпдкЪ§жсЕФЩЯЗНзїе§ЗНаЮABCD.ЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂ,вдУПУы
ГіЗЂ,вдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсе§ЗНЯђдШЫйдЫЖЏЃЌЭЌЪБЖЏЕу
ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсе§ЗНЯђдШЫйдЫЖЏЃЌЭЌЪБЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂ,вдУПУы
ГіЗЂ,вдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕу
ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕу![]() дШЫйдЫЖЏЃЌЕНДя
дШЫйдЫЖЏЃЌЕНДя![]() ЕуКѓдйвдЭЌбљЕФЫйЖШбиЪ§жсе§ЗНЯђдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ
ЕуКѓдйвдЭЌбљЕФЫйЖШбиЪ§жсе§ЗНЯђдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ![]() Уы
Уы![]() .
.
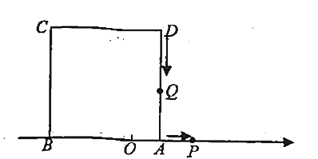
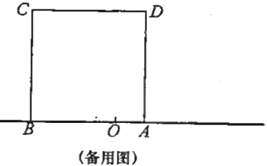
(1)ШєЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() .ЩЯдЫЖЏЃЌЕБtЮЊКЮжЕЪБ,
.ЩЯдЫЖЏЃЌЕБtЮЊКЮжЕЪБ,![]() ?
?
(2)ШєЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯдЫЖЏЃЌСЌНг
ЩЯдЫЖЏЃЌСЌНг![]() ,ЕБtЮЊКЮжЕЪБ,Ш§НЧаЮ
,ЕБtЮЊКЮжЕЪБ,Ш§НЧаЮ![]() ЕФУцЛ§ЕШгке§ЗНаЮ
ЕФУцЛ§ЕШгке§ЗНаЮ![]() УцЛ§ЕФ
УцЛ§ЕФ![]() ?
?
(3)дкЕу![]() КЭЕу
КЭЕу![]() дЫЖЏЕФЙ§ГЬжаЃЌЕБ
дЫЖЏЕФЙ§ГЬжаЃЌЕБ![]() ЮЊКЮжЕЪБЃЌЕу
ЮЊКЮжЕЪБЃЌЕу![]() гыЕу
гыЕу![]() ЧЁКУжиКЯ?
ЧЁКУжиКЯ?
(4)ЕБЕу![]() дкЪ§жсЩЯдЫЖЏЪБЃЌЪЧЗёДцдкФГ-ЪБПЬt,ЪЙЕУЯпЖЮ
дкЪ§жсЩЯдЫЖЏЪБЃЌЪЧЗёДцдкФГ-ЪБПЬt,ЪЙЕУЯпЖЮ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ,ШєДцдкЃЌЧѓГі
,ШєДцдкЃЌЧѓГі![]() ЕФжЕ;ШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФжЕ;ШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ4ЃЛЃЈ4ЃЉДцдкЃЌt=3Лђ5ЃЌРэгЩМћЯъНт.
ЃЛЃЈ3ЃЉ4ЃЛЃЈ4ЃЉДцдкЃЌt=3Лђ5ЃЌРэгЩМћЯъНт.
ЁОНтЮіЁП
(1)гЩЪ§жсЩЯЕу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ,Еу
,Еу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ,вд
,вд![]() ЮЊБпдкЪ§жсЕФЩЯЗНзїе§ЗНаЮABCDЃЌ
ЮЊБпдкЪ§жсЕФЩЯЗНзїе§ЗНаЮABCDЃЌ![]() ЃЌСаГіЗНГЬЃЌМДПЩЧѓНтЃЛ
ЃЌСаГіЗНГЬЃЌМДПЩЧѓНтЃЛ
(2)ИљОнШ§НЧаЮ![]() ЕФУцЛ§ЕШгке§ЗНаЮ
ЕФУцЛ§ЕШгке§ЗНаЮ![]() УцЛ§ЕФ
УцЛ§ЕФ![]() ЃЌСаГіЗНГЬЃЌМДПЩЃЛ
ЃЌСаГіЗНГЬЃЌМДПЩЃЛ
(3)ИљОнЕШСПЙиЯЕЃЌСаГіЗНГЬМДПЩЧѓНтЃЛ
(4)ЗжСНжжЧщПіЃКЂйЕБЕуQдкЕуPЕФзѓВрЪБЃЌ ЂкЕБЕуQдкЕуPЕФгвВрЪБЃЌЗжБ№СаГіЗНГЬЃЌМДПЩЧѓНт.
ЃЈ1ЃЉЁпЪ§жсЩЯЕу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ,Еу
,Еу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ,вд
,вд![]() ЮЊБпдкЪ§жсЕФЩЯЗНзїе§ЗНаЮABCDЃЌ
ЮЊБпдкЪ§жсЕФЩЯЗНзїе§ЗНаЮABCDЃЌ
ЁрAD=AB=4ЃЌ
ЁрAQ=4-2tЃЌAP=tЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр4-2t =tЃЌНтЕУЃКt=![]() ЃЌ
ЃЌ
ЁрЕБt=![]() УыЪБЃЌ
УыЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпAQ=4-2tЃЌAB=4ЃЌ
Ёр![]() ЃЌе§ЗНаЮ
ЃЌе§ЗНаЮ![]() УцЛ§=4ЁС4=16ЃЌ
УцЛ§=4ЁС4=16ЃЌ
Ёр8-4t=![]() ЃЌНтЕУЃКt=
ЃЌНтЕУЃКt=![]() ЃЌ
ЃЌ
ЁрЕБt=![]() УыЪБЃЌШ§НЧаЮ
УыЪБЃЌШ§НЧаЮ![]() ЕФУцЛ§ЕШгке§ЗНаЮ
ЕФУцЛ§ЕШгке§ЗНаЮ![]() УцЛ§ЕФ
УцЛ§ЕФ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉИљОнЬтвтЕУЃК2t-4=tЃЌНтЕУЃКt=4ЃЌ
ЁрЕБt=4УыЪБЃЌЕу![]() гыЕу
гыЕу![]() ЧЁКУжиКЯЃЛ
ЧЁКУжиКЯЃЛ
ЃЈ4ЃЉЂйЕБЕуQдкЕуPЕФзѓВрЪБЃЌt-ЃЈ2t-4ЃЉ=1ЃЌНтЕУЃКt=3ЃЌ
ЂкЕБЕуQдкЕуPЕФгвВрЪБЃЌЃЈ2t-4ЃЉ-t=1ЃЌНтЕУЃКt=5ЃЌ
ЁрЕБt=3УыЛђ5УыЪБЃЌЯпЖЮ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕу
ГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕу![]() дЫЖЏЃЌЭЌЪБЃЌЕу
дЫЖЏЃЌЭЌЪБЃЌЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕу
ГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕу![]() дЫЖЏ.ЦфжавЛИіЖЏЕуЕНДяжеЕуЪБЃЌСэвЛИіЖЏЕувВЫцжЎЭЃжЙдЫЖЏ.Й§Еу
дЫЖЏ.ЦфжавЛИіЖЏЕуЕНДяжеЕуЪБЃЌСэвЛИіЖЏЕувВЫцжЎЭЃжЙдЫЖЏ.Й§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЩшдЫЖЏЪБМфЮЊ
ЃЌЩшдЫЖЏЪБМфЮЊ![]() Уы.
Уы.
(1)СЌНг![]() ЁЂ
ЁЂ![]() ЃЌЕБ
ЃЌЕБ![]() ЮЊКЮжЕЪБЃЌЫФБпаЮ
ЮЊКЮжЕЪБЃЌЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЃЛ
ЮЊЦНааЫФБпаЮЃЛ
(2)ЧѓГіЕу![]() ЕН
ЕН![]() ЕФОрРыЃЛ
ЕФОрРыЃЛ
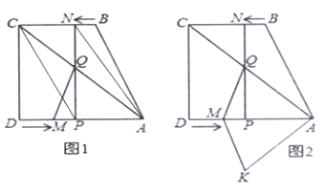
(3)ШчЭМ2ЃЌНЋ![]() би
би![]() ЗелЃЌЕУ
ЗелЃЌЕУ![]() ЃЌЪЧЗёДцдкФГЪБПЬ
ЃЌЪЧЗёДцдкФГЪБПЬ![]() ЃЌЪЙЫФБпаЮ
ЃЌЪЙЫФБпаЮ![]() ЮЊСтаЮЃЌШєДцдкЃЌЧѓ
ЮЊСтаЮЃЌШєДцдкЃЌЧѓ![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїгУГпЙцзїЭМзїЁїABCБпACЩЯЕФИпBHЃЌзїЗЈШчЯТЃК
ЂйЗжБ№вдЕуDЃЌEЮЊдВаФЃЌДѓгк![]() DEЕФГЄЮЊАыОЖзїЛЁЃЌСНЛЁНЛгкFЃЛ
DEЕФГЄЮЊАыОЖзїЛЁЃЌСНЛЁНЛгкFЃЛ
ЂкзїЩфЯпBFЃЌНЛБпACгкЕуHЃЛ
ЂлвдBЮЊдВаФЃЌBKГЄЮЊАыОЖзїЛЁЃЌНЛжБЯпACгкЕуDКЭEЃЛ
ЂмШЁвЛЕуKЃЌЪЙKКЭBдкACЕФСНВрЃЛ
ЫљвдЃЌBHОЭЪЧЫљЧѓзїЕФИпЃЎ ЦфжаЫГађе§ШЗЕФзїЭМВНжшЪЧЃЈЁЁЁЁЃЉ

A. ЂйЂкЂлЂм B. ЂмЂлЂкЂй C. ЂкЂмЂлЂй D. ЂмЂлЂйЂк
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
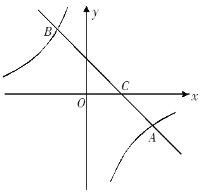
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§y =ax+bЕФЭМЯёгыЗДБШР§КЏЪ§y =![]() ЕФЭМЯёНЛгкAЃЈ4ЃЌЉ2ЃЉЁЂBЃЈЉ2ЃЌmЃЉСНЕуЃЌгыxжсНЛгкЕуC.
ЕФЭМЯёНЛгкAЃЈ4ЃЌЉ2ЃЉЁЂBЃЈЉ2ЃЌmЃЉСНЕуЃЌгыxжсНЛгкЕуC.
ЃЈ1ЃЉЧѓaЃЌmЕФжЕЃЛ
ЃЈ2ЃЉЧыжБНгаДГіВЛЕШЪНax+bЁн![]() ЕФНтМЏЃЛ
ЕФНтМЏЃЛ
ЃЈ3ЃЉЕуPдкЗДБШР§КЏЪ§ЭМЯёЩЯЃЌЧвЕуPЕФКсзјБъЮЊЃ4ЃЌдкЦНУцжБНЧзјБъЯЕжаЪЧЗёДцдквЛЕуQЃЌЪЙЕУвдAЁЂBЁЂPЁЂQЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃПШчЙћДцдкЃЌЧыжБНгаДГіЕуQЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАбОиаЮжНЦЌOABCЗХШыЦНУцжБНЧзјБъЯЕжаЃЌЪЙOAЁЂOCЗжБ№ТфдкxжсЃЌyжсЩЯЃЌСЌOBЃЌНЋжНЦЌOABCбиOBелЕўЃЌЪЙЕуAТфдкAЁфЕФЮЛжУЃЌШєOB=![]() ЃЌtanЁЯBOC=
ЃЌtanЁЯBOC=![]() ЃЌдђЕуAЁфЕФзјБъЃЈЁЁЁЁЃЉ
ЃЌдђЕуAЁфЕФзјБъЃЈЁЁЁЁЃЉ

A. ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ B. ЃЈЉ
ЃЉ B. ЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉ C. ЃЈЉ
ЃЉ C. ЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉ D. ЃЈЉ
ЃЉ D. ЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCЕФШ§ИіЖЅЕуЗжБ№ЮЊAЃЈ1ЃЌ2ЃЉЃЌBЃЈ2ЃЌ5ЃЉЃЌCЃЈ6ЃЌ1ЃЉЃЎШєКЏЪ§y=![]() дкЕквЛЯѓЯоФкЕФЭМЯѓгыЁїABCгаНЛЕуЃЌдђkЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
дкЕквЛЯѓЯоФкЕФЭМЯѓгыЁїABCгаНЛЕуЃЌдђkЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГФІЭаГЕГЇБОжмМЦЛЎУПШеЩњВњ450СОФІЭаГЕЃЌгЩгкЙЄШЫЪЕааТжанЃЌ УПШеЩЯАрШЫЪ§ВЛвЛЖЈЯрЕШЃЌЪЕМЪУПШеЩњВњСПгыМЦЛЎСПЯрБШЧщПіШчЯТБэЃК [діМгЕФСОЪ§ЮЊе§Ъ§ЃЌМѕЩйЕФСОЪ§ЮЊИКЪ§]
аЧЦк | вЛ | Жў | Ш§ | ЫФ | Юх | Сљ | Ше |
діМѕ | Ѓ5 | +7 | Ѓ3 | +4 | +10 | Ѓ9 | Ѓ25 |
ЃЈ1ЃЉБОжмаЧЦкСљЩњВњЖрЩйСОФІЭаГЕЃП
ЃЈ2ЃЉБОжмзмВњСПгыМЦЛЎВњСПЯрБШЃЌЪЧдіМгСЫЛЙЪЧМѕЩйСЫЃПЮЊЪВУД?
ЃЈ3ЃЉВњСПзюЖрЕФФЧЬьБШВњСПзюЩйЕФФЧЬьЖрЩњВњЖрЩйСОЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМOЮЊжБЯпABЩЯвЛЕуЃЌЁЯAOCЃН50ЁуЃЌODЦНЗжЁЯAOCЃЌЁЯDOEЃН90ЁуЃЎ

ЃЈ1ЃЉЧѓЁЯBODЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЪдХаЖЯOEЪЧЗёЦНЗжЁЯBOCЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєНЋДњЪ§ЪНжаЕФШЮвтСНИізжФИНЛЛЛЃЌДњЪ§ЪНВЛБфЃЌдђГЦетИіДњЪ§ЪНЮЊЭъШЋЖдГЦЪНЃЌШч![]() ОЭЪЧЭъШЋЖдГЦЪН(ДњЪ§ЪНжа
ОЭЪЧЭъШЋЖдГЦЪН(ДњЪ§ЪНжа![]() ЛЛГЩbЃЌbЛЛГЩ
ЛЛГЩbЃЌbЛЛГЩ![]() ЃЌДњЪ§ЪНБЃГжВЛБф).ЯТСаШ§ИіДњЪ§ЪНЃКЂй
ЃЌДњЪ§ЪНБЃГжВЛБф).ЯТСаШ§ИіДњЪ§ЪНЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЎЦфжаЪЧЭъШЋЖдГЦЪНЕФЪЧЃЈ ЃЉ
ЃЎЦфжаЪЧЭъШЋЖдГЦЪНЕФЪЧЃЈ ЃЉ
A.ЂйЂкB.ЂйЂлC.ЂкЂлD.ЂйЂкЂл
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com