
【题目】在如图平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,
,![]() 、
、![]() 分别落在
分别落在![]() 轴和
轴和![]() 轴上,
轴上,![]() 是矩形的对角线. 将
是矩形的对角线. 将![]() 绕点
绕点![]() 逆时针旋转,使点
逆时针旋转,使点![]() 落在
落在![]() 轴上,得到
轴上,得到![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,交
,交![]() 于点
于点![]() .
.

(1)求![]() 的值和点
的值和点![]() 的坐标;
的坐标;
(2)连接![]() ,则图中是否存在与
,则图中是否存在与![]() 相似的三角形?若存在,请把它们一一找出来,并选其中一种进行证明;若不存在,请说明理由;
相似的三角形?若存在,请把它们一一找出来,并选其中一种进行证明;若不存在,请说明理由;
(3)在线段![]() 上存在这样的点
上存在这样的点![]() ,使得
,使得![]() 是等腰三角形,请直接写出点
是等腰三角形,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ,G
,G![]() ;(2)
;(2)![]() ,
,![]() ,
, ![]() ,证明见解析;(3)
,证明见解析;(3)![]()
![]() 或
或![]() 或
或
【解析】
(1)证明△COF∽△AOB,则![]() ,求得:点F的坐标为(1,2),即可求解;
,求得:点F的坐标为(1,2),即可求解;
(2)△COF∽△BFG;△AOB∽△BFG;△ODE∽△BFG;△CBO∽△BFG.证△OAB∽△BFG: ,即可求解.
,即可求解.
(3)分GF=PF、PF=PG、GF=PG三种情况,分别求解即可.
(1)∵四边形![]() 为矩形,点
为矩形,点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 旋转得到的,即:
旋转得到的,即:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∵![]() 的图象经过点
的图象经过点![]() ,
,
∴![]() ,得
,得![]() ,
,
∵点![]() 在
在![]() 上,
上,
∴点![]() 的横坐标为4,
的横坐标为4,
对于![]() ,当
,当![]() ,得
,得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
(2)![]() ;
;![]() ;
; ![]() ;
;![]() .
.
下面对![]() 进行证明:
进行证明:
∵点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() .
.
∴![]() ,
, .
.
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
(3)设点![]() ,而点
,而点![]() 、点
、点![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
当![]() 时,即
时,即![]() ,解得:
,解得:![]() (舍去负值);
(舍去负值);
当![]() 时,同理可得:
时,同理可得:![]() ;
;
当![]() 时,同理可得:
时,同理可得:![]() (舍去正值);
(舍去正值);
综上,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,E,F分别是线段CD和线段BA延长线上的动点,沿直线EF折叠使点D的对应点D′落在BC上,连接AD′,DD′,当△ADD′是以DD′为腰的等腰三角形时,DE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,直角三角板ABC中,∠C=90°,AC=BC,将一个用足够长的的细铁丝制作的直角的顶点D放在直角三角板ABC的斜边AB上,再将该直角绕点D旋转,并使其两边分别与三角板的AC边、BC边交于P、Q两点.
问题探究:(1)在旋转过程中,
①如图2,当AD=BD时,线段DP、DQ有何数量关系?并说明理由.
②如图3,当AD=2BD时,线段DP、DQ有何数量关系?并说明理由.
③根据你对①、②的探究结果,试写出当AD=nBD时,DP、DQ满足的数量关系为_______________(直接写出结论,不必证明)
(2)当AD=BD时,若AB=20,连接PQ,设△DPQ的面积为S,在旋转过程中,S是否存在最小值或最大值?若存在,求出最小值或最大值;若不存在,请说明理由.

图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.
(1)求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;
(2)若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
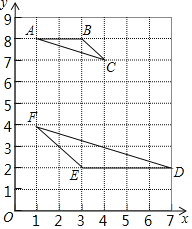
【题目】如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点![]() 每个小方格的顶点叫格点
每个小方格的顶点叫格点![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
![]() 外接圆的圆心坐标是______;
外接圆的圆心坐标是______;
![]() 外接圆的半径是______;
外接圆的半径是______;
![]() 已知
已知![]() 与
与![]() 点D、E、F都是格点
点D、E、F都是格点![]() 成位似图形,则位似中心M的坐标是______;
成位似图形,则位似中心M的坐标是______;
![]() 请在网格图中的空白处画一个格点
请在网格图中的空白处画一个格点![]() ,使
,使![]() ∽
∽![]() ,且相似比为
,且相似比为![]() :1.
:1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目:初中数学 来源: 题型:
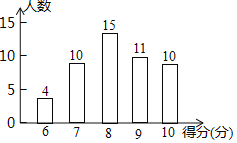
【题目】为了了解居民的环保意识,社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动,并用得到的数据绘制了如图条形统计图(得分为整数,满分为10分,最低分为6分)请根据图中信息,解答下列问题:
(1)本次调查一共抽取了 名居民;
(2)直接写出本次调查获取的样本数据的平均数为 ,中位数为 ;
(3)社区决定对该小区1500名居民开展这项有奖问答活动,得10分者设为“一等奖”,请你根据调查结果,帮社区工作人员估计需准备多少份“一等奖”奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c过点A(3, 0)、点B(0, 3).点M(m, 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P,与抛物线交于点Q,联结BQ.
x2+bx+c过点A(3, 0)、点B(0, 3).点M(m, 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P,与抛物线交于点Q,联结BQ.
(1)求抛物线表达式;
(2)联结OP,当∠BOP=∠PBQ时,求PQ的长度;
(3)当△PBQ为等腰三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
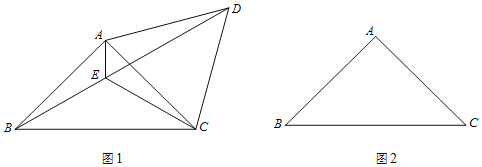
【题目】已知:在△ABC中,∠BAC=90°,AB=AC.
(1)如图1,将线段AC绕点A逆时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD于点E,连结CE.
①求证:∠AED=∠CED;
②用等式表示线段AE、CE、BD之间的数量关系(直接写出结果);
(2)在图2中,若将线段AC绕点A顺时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD的延长线于点E,连结CE.请补全图形,并用等式表示线段AE、CE、BD之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com