
【题目】如图,二次函数y=x2﹣m2(m>0且为常数)的图象与x轴交于点A、B(A在B左侧),与y轴交于C.
(1)求A,B,C三点的坐标(用含m的式子表示);
(2)若∠ACB=90°,求m的值.
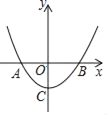
【答案】(1) A(﹣m,0),B(m,0),C(0,﹣m2);(2) m的值为1.
【解析】
(1)令y=0,解方程x2﹣m2=0,可求出点A和点B的坐标;令当x=0,解方程x2﹣m2=0,可求出点C的坐标;
(2)由∠ACB=90°及二次函数的对称性可证明△BOC是等腰直角三角形,从而可得m2=m,进而可求出m的值.
(1)当y=0时,x2﹣m2=0,解得x1=﹣m,x2=m,则A(﹣m,0),B(m,0),
当x=0时,y=x2﹣m2=﹣m2,则C(0,﹣m2);
(2)∵∠ACB=90°,OC⊥AB,OA=OB,
∴∠CBO=45 ,
∴△BOC是等腰直角三角形,
∴OC=OB,
∴m2=m,解得m1=0(舍去),m2=1,
∴m的值为1.


科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,∠ABC=90,AE∥CD交BC于E,O是AC的中点,AB=![]() ,AD=2,BC=3,下列结论:
,AD=2,BC=3,下列结论:
①∠CAE=30;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正确的是()

A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
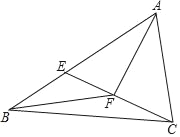
【题目】△ABC中,AB=CB,AC=10,S△ABC=60,E为AB上一动点,连结CE,过A作AF⊥CE于F,连结BF,则BF的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
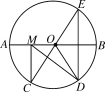
【题目】如图,在⊙O中,AB是⊙O的直径,AB=10,![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用![]() 元购进某种干果销售,由于销售状况良好,超市又调拨
元购进某种干果销售,由于销售状况良好,超市又调拨![]() 元资金购进该种干果,但这次的进价比第一次的进价提高了
元资金购进该种干果,但这次的进价比第一次的进价提高了![]() ,购进干果数量是第一次的
,购进干果数量是第一次的![]() 倍还多
倍还多![]() 千克.
千克.
![]() 该种干果的第一次进价是每千克多少元?
该种干果的第一次进价是每千克多少元?
![]() 如果超市将这种干果全部按每千克
如果超市将这种干果全部按每千克![]() 元的价格出售,售完这种干果共盈利多少元?
元的价格出售,售完这种干果共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c.
(Ⅰ)若抛物线的顶点为A(﹣2,﹣4),抛物线经过点B(﹣4,0)
①求该抛物线的解析式;
②连接AB,把AB所在直线沿y轴向上平移,使它经过原点O,得到直线l,点P是直线l上一动点.
设以点A,B,O,P为顶点的四边形的面积为S,点P的横坐标为x,当4+6![]() ≤S≤6+8
≤S≤6+8![]() 时,求x的取值范围;
时,求x的取值范围;
(Ⅱ)若a>0,c>1,当x=c时,y=0,当0<x<c时,y>0,试比较ac与l的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
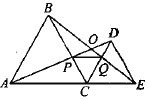
【题目】如图,![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),在
重合),在![]() 同侧分别作等边
同侧分别作等边![]() 和等边
和等边![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .下列五个结论:①
.下列五个结论:①![]() ;②
;②![]() ;③
;③![]() ;④DE=DP;⑤
;④DE=DP;⑤![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了![]() 箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
第 | 第 | 第 | 第 | 第 | |
甲成绩 |
|
|
|
|
|
乙成绩 |
|
|
|
|
|
(1)a=_________
(2)![]()
(3)参照小宇的计算方法,计算乙成绩的方差;
(4)请你从平均数和方差的角度分析,谁将被选中.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是关于
是关于![]() 的方程
的方程![]() 的两实根,实数
的两实根,实数![]() 、
、![]() 、
、![]() 、
、![]() 的大小关系可能是( )
的大小关系可能是( )
A. α<a<b<β B. a<α<β<b C. a<α<b<β D. α<a<β<b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com