
【题目】如图,抛物线y=nx2﹣3nx﹣4n(n<0)与x轴交于B、C两点(点B在点C的左侧),且抛物线与y轴交于点A.
(1)点B的坐标为 ,点C的坐标为 ;
(2)若∠BAC=90°,求抛物线的解析式.
(3)点M是(2)中抛物线上的动点,点N是其对称轴上的动点,是否存在这样的点M、N,使得以A、C、M、N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.

【答案】(1)(﹣1,0),(4,0);(2)y=﹣![]() x2+
x2+![]() x+2;(3)点M的坐标分别为:(﹣
x+2;(3)点M的坐标分别为:(﹣![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)利用x轴上点的坐标特点即可得出结论;
(2)判断出△AOB∽△COA,建立方程求出OA,进而得出点A坐标,最后用待定系数法即可的结论;
(3)设出点M,N的坐标,分三种情况,利用中点坐标公式建立方程求解即可得出结论.
(1)令y=0,
∴nx2-3nx-4n=0,
∵n<0,
∴x2-2x-4=0,
∴x=-1或x=4,
∴B(-1,0),C(4,0);
(2)∵∠BAC=90°,AO⊥BC,
易证△AOB~△COA,
∴![]() ,
,![]() ,
,
∴OA=2,
故A(0,2),
则设抛物线的解析式为:y=a(x-x1)( x-x2),
把A(0,2)、B(-1,0)、C(4,0)代入上式得,-4a=2,
∴![]() ,
,
∴![]() ,
,
∴对称轴直线为![]() ,
,
∴设N(![]() ,b),M(m,
,b),M(m,![]() ),
),
以A、C、M、N为顶点的四边形是平行四边形,
∴①当AC为对角线时,![]() ,
,
∴![]() .
.
∴M(![]() ,
,![]() ).
).
②当AM为对角线时,![]() ,
,
∴![]() .
.
∴M(![]() ,-
,-![]() ).
).
③当AN为对角线时,![]() ,
,
∴![]() .
.
∴M(![]() ,-
,-![]() ).
).
即:抛物线上存在这样的点M,点M的坐标分别为:M(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() )或(
)或(![]() ,-
,-![]() ).
).


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 中,∠ABC=90°,AB=BC= ![]() ,三角形的顶点在相互平行的三条直线l1、l2、l3 上,且 l2、l3之间的距离为 2,则 l1、l2 之间的距离为______.
,三角形的顶点在相互平行的三条直线l1、l2、l3 上,且 l2、l3之间的距离为 2,则 l1、l2 之间的距离为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】测量物体高度
![]() 小明想测量一棵树的高度
小明想测量一棵树的高度![]() ,在阳光下,小明测得一根长为
,在阳光下,小明测得一根长为![]() 米的竹竿的影长为
米的竹竿的影长为![]() 米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为
米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为![]() 米,落在地面上的影长为
米,落在地面上的影长为![]() 米,则树高
米,则树高![]() 为多少米.
为多少米.
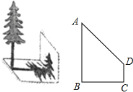
![]() 小明在某一时刻测得
小明在某一时刻测得![]() 的杆子在阳光下的影子长为
的杆子在阳光下的影子长为![]() ,他想测量电线杆
,他想测量电线杆![]() 的高度,但其影子恰好落在土坡的坡面
的高度,但其影子恰好落在土坡的坡面![]() 和地面
和地面![]() 上,量得
上,量得![]() ,
,![]() ,
,![]() 与地面成
与地面成![]() .
.
求电线杆的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋节是我国的传统节日,人们素有吃月饼的习俗.某超市在中秋节来临之际用3000元购进A、B两种月饼1100个,若购买A种月饼与购买B种月饼的费用相同,且A种月饼的单价是B种月饼单价的1.2倍.
(1)求A、B两种月饼的单价各是多少?
(2)若计划用不超过7000元的资金再次购进A、B两种月饼共2600个,已知A、B两种月饼的进价不变.求A种月饼最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线BC:![]() ,直线BD与x轴交于点A,点B(2,3),点D(0,
,直线BD与x轴交于点A,点B(2,3),点D(0,![]() ).
).
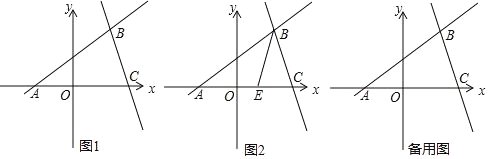
(1)求直线BD的函数解析式;
(2)在y轴上找一点P,使得△ABC与△ACP的面积相等,求出点P的坐标;
(3)如图2,E为线段AC上一点,连结BE,一动点F从点B出发,沿线段BE以每秒1个单位运动到点E再沿线段EA以每秒![]() 个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.
个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)为加强与家长的沟通,某校在家长会到来之前需印刷《致家长的一封信》等材料以作宣传,该校的印刷任务原来由甲复印店承接,其收费y(元)与印刷页数x(页)的函数关系如图所示.

(1)从图象中可看出:印刷超过500页部分每页收费 元;
(2)现在乙印刷厂表示:每页0.15元收费.另收200元的制版费,乙印刷厂收费y(元)与印刷页数x(页)的函数关系为 ;
(3)在给出的坐标系内画出(2)中的函数图象,并结合函数图象回答印刷页数在3000页左右应选择哪个印刷店?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE中,AB=AD=6,BC=DE,∠B=∠D=30°,边AD与边BC交于点P(不与点B,C重合),点B,E在AD异侧,I为△APC的内心.
(1)求证:∠BAD=∠CAE;
(2)设AP=x,请用含x的式子表示PD,并求PD的最大值;
(3)当AB⊥AC时,∠AIC的取值范围为m°<∠AIC<n°,分别直接写出m,n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般地,“任意三角形都是自相似图形”,只要顺次连接三角形各边中点,则可将原三角形分割为四个都与它自己相似的小三角形.我们把![]() (图乙)第一次顺次连接各边中点所进行的分割,称为
(图乙)第一次顺次连接各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() );把
);把![]() 阶分割得出的
阶分割得出的![]() 个三角形再分别顺次连接它的各边中点所进行的分割,称为
个三角形再分别顺次连接它的各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() )…,依此规则操作下去.
)…,依此规则操作下去.![]() 阶分割后得到的每一个小三角形都是全等三角形(
阶分割后得到的每一个小三角形都是全等三角形(![]() 为正整数),设此时小三角形的面积为
为正整数),设此时小三角形的面积为![]() .请写出一个反映
.请写出一个反映![]() ,
,![]() ,
,![]() 之间关系的等式________.
之间关系的等式________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com