
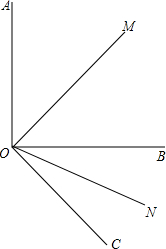
 如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC.
如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC.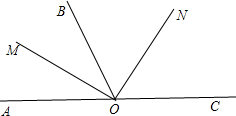
 ∠AOB=45°,∠NOB=
∠AOB=45°,∠NOB= ∠BOC=15°,
∠BOC=15°, ∠AOB=
∠AOB= α,∠NOB=
α,∠NOB= ∠BOC=
∠BOC= β,
β, α+
α+ β=
β= (α+β);
(α+β); ∠AOB,∠NOB=
∠AOB,∠NOB= ∠BOC,
∠BOC, (∠AOB+∠BOC)=
(∠AOB+∠BOC)= ∠AOC=90°.
∠AOC=90°. ∠AOB=45°,∠NOB=
∠AOB=45°,∠NOB= ∠BOC=15°,则∠MON=∠BOM+∠BON=60°;
∠BOC=15°,则∠MON=∠BOM+∠BON=60°; ∠AOB=
∠AOB= α,∠NOB=
α,∠NOB= ∠BOC=
∠BOC= β,则∠MON=∠BOM+∠BON=
β,则∠MON=∠BOM+∠BON= α+
α+ β=
β= (α+β);
(α+β); ∠AOB,∠NOB=
∠AOB,∠NOB= ∠BOC,所以∠MON=∠BOM+∠BON=
∠BOC,所以∠MON=∠BOM+∠BON= (∠AOB+∠BOC)=
(∠AOB+∠BOC)= ∠AOC.
∠AOC.

科目:初中数学 来源:1+1轻巧夺冠·优化训练(冀教版)七年级数学(下) 冀教版银版 题型:022
如图所示,已知AO⊥BC,垂足为O,且∠COD-∠DOA=30°,则∠BOD=________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com