Question

如图，双曲线经过的两个顶点、轴，连接，将沿翻折后得到，点刚好落在线段上，连接，恰好平分与轴负半轴的夹角，若的面积为3，则的值为          。

Answer 1

-6.

解析试题分析：设BC的延长线交x轴于点D，连接OC，点C（-m，n），AB=a，由角平分线的性质得，CD=CB′，则△OCD≌△OCB′，再由翻折的性质得，BC=B′C，根据反比例函数的性质，可得出S_△OCD=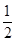mn=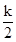，由AB∥x轴，得点A（a-m，2n），由题意得2n（a-m）=k，即可得出答案．
试题解析：如图：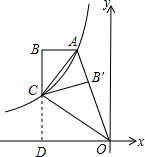

设BC的延长线交x轴于点D，
设点C（-m，n），AB=a，
∵∠ABC=90°，AB∥x轴，
∴CD⊥x轴，
由折叠的性质可得：∠AB′C=∠ABC=90°，
∴CB′⊥OA，
∵OC平分OA与x轴负半轴的夹角，
∴CD=CB′，
在Rt△OB′C和Rt△ODC中，
∵,
∴Rt△OCD≌Rt△OCB′（HL），
再由翻折的性质得，BC=B′C，
∴BC=CD，
∴点B（-m，2n）
∵双曲线经过Rt△ABC的两个顶点A、C,
∴S_△OCD=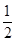|mn|=|k|
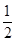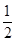∴mn=k
∵AB∥x轴，
∴点A（a-m，2n），
∴2n（a-m）=k
∴an=k
∴k=-6
考点: 反比例函数综合题．