

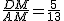 或sin∠DAB′=
或sin∠DAB′= 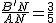 .
.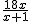 或 y=
或 y= 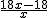 .
.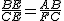 .
.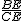 =2,∴CF=3;∵AB∥CF,∴∠BAE=∠F;又∠BAE=∠B′AE,∴∠B′AE=∠F,∴MA=MF.
=2,∴CF=3;∵AB∥CF,∴∠BAE=∠F;又∠BAE=∠B′AE,∴∠B′AE=∠F,∴MA=MF.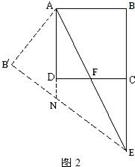 令MA=MF=k,则MC=k-3,DM=9-k.
令MA=MF=k,则MC=k-3,DM=9-k.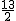 ,∴DM=
,∴DM= 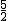 .……3’∴sin∠DAB′=
.……3’∴sin∠DAB′= 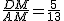 .……4’
.……4’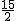 , ∴B′N=
, ∴B′N= 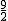 ,在Rt△AB′N中,由勾股定理,得m2=(12-m)2+62,
,在Rt△AB′N中,由勾股定理,得m2=(12-m)2+62,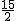 ,∴B′N=
,∴B′N= 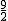 ,……5’∴sin∠DAB′=
,……5’∴sin∠DAB′= 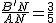 .………6’
.………6’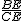 =x时,正方形ABCD的边长为6cm,△ABE翻折后与正方形ABCD公共部分的面积y.当点E在BC上时.∵
=x时,正方形ABCD的边长为6cm,△ABE翻折后与正方形ABCD公共部分的面积y.当点E在BC上时.∵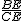 =x,∴
=x,∴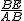 =
= 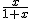 ,BE=
,BE= 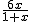 ,∴y=
,∴y= 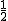 ×AB×BE,即y=
×AB×BE,即y= 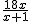 .…8’
.…8’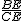 =x,∴
=x,∴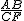 =
= 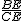 ,又∵AD=6,∴FC=
,又∵AD=6,∴FC= 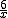 ,DF="6-"
,DF="6-" 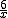 ;∴
;∴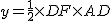 ,
,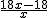 .
.

科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.正三角形 | B.正方形 | C.正五边形 | D.正六边形 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
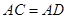 ,
,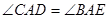 ,
,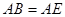
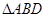 ≌
≌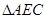 ;
;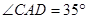 ,
,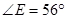 ,
,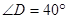 ,
,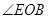 的度数
的度数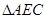 绕点A逆时针旋转
绕点A逆时针旋转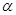 度(
度(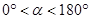 ),问当
),问当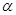 为多少度时,直线CE分别与
为多少度时,直线CE分别与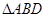 的三边所在的直线垂直?(请直接写出答案)。
的三边所在的直线垂直?(请直接写出答案)。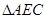 绕点A逆时针旋转后得到
绕点A逆时针旋转后得到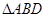 ,并使点D,E,A三点在同一条直线上,若
,并使点D,E,A三点在同一条直线上,若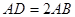 ,连接CD,若
,连接CD,若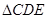 的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。
的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。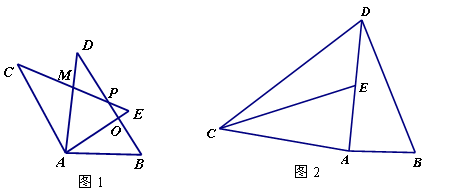
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com