
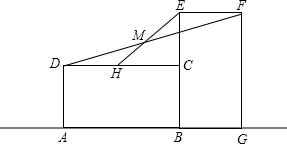
 (1)若点M是线段DF的中点,连接EM并延长交DC于点H,试说明EM=MH;
(1)若点M是线段DF的中点,连接EM并延长交DC于点H,试说明EM=MH;
|
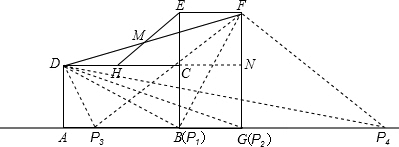
| DN2+FN2 |
| 32+12 |
| 10 |
| PF2-FG2 |
|
| 6 |
| 6 |
| 6 |
| 6 |
| 6 |


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
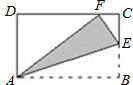 如图,将矩形ABCD的BC边折起,使点B落在DC上的点F处得折痕AE,若∠DFA为40°,则∠EAF的度数是( )
如图,将矩形ABCD的BC边折起,使点B落在DC上的点F处得折痕AE,若∠DFA为40°,则∠EAF的度数是( )| A、15° | B、20° | C、25° | D、30° |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,将矩形ABCD绕C点顺时针旋转到矩形CEFG,点E在CD上,若AB=8,BC=6,则旋转过程中点A所经过的路径长为
如图,将矩形ABCD绕C点顺时针旋转到矩形CEFG,点E在CD上,若AB=8,BC=6,则旋转过程中点A所经过的路径长为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com