
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНx2Љ2mx+m2Љ2гыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉХзЮяЯпЕФЖЅЕузјГЦЮЊЁЁ ЁЁЃЌЕуCзјБъЮЊЁЁ ЁЁЃЛЃЈгУКЌmЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉЕБmЃН1ЪБЃЌХзЮяЯпЩЯгавЛЖЏЕуPЃЌЩшPЕуКсзјБъЮЊnЃЌЧвnЃО0ЃЎ
ЂйШєЕуPЕНxжсЕФОрРыЮЊ2ЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЂкЩшХзЮяЯпдкЕуCгыЕуPжЎМфВПЗжЃЈКЌЕуCКЭЕуPЃЉзюИпЕугызюЕЭЕузнзјБъжЎВюЮЊhЃЌЧѓhгыnжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПnЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШєЕуAЃЈЉ3ЃЌ2ЃЉЁЂBЃЈ2ЃЌ2ЃЉЃЌСЌНсABЃЌЕБХзЮяЯпyЃНx2Љ2mx+m2Љ2гыЯпЖЮABжЛгавЛИіНЛЕуЪБЃЌжБНгаДГіmЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈmЃЌЉ2ЃЉЃЌЃЈ0ЃЌm2Љ2ЃЉЃЌЃЈ2ЃЉЂйP1ЃЈ1ЃЌЉ2ЃЉЃЌP2ЃЈ3ЃЌ2ЃЉЃЛЂк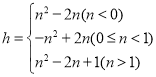 ЃЛЃЈ3ЃЉmЕФШЁжЕЗЖЮЇЮЊЉ5ЁмmЃМЉ1Лђ0ЃМmЁм4ЃЎ
ЃЛЃЈ3ЃЉmЕФШЁжЕЗЖЮЇЮЊЉ5ЁмmЃМЉ1Лђ0ЃМmЁм4ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЕБxЃН0ЪБЃЌЧѓГіyЕФжЕЃЌМДПЩаДГіЕуCзјБъЃЌНЋХзЮяЯпyЃНx2Љ2mx+m2Љ2ЛЏЮЊЖЅЕуЪНМДПЩаДГіЖЅЕузјБъЃЛ
ЃЈ2ЃЉЂйЕБmЃН1ЪБЃЌЯШЧѓГіХзЮяЯпЕФНтЮіЪНЃЌдйЗжБ№НЋyЃНЁР2ДњШыНтЮіЪНМДПЩЧѓГіЕуPзјБъЃЛ
ЂкгУКЌnЕФДњЪ§ЪНБэЪОГіЕуPЕФзјБъЃЌЗжЕуPдкyжсзѓВрЃЌдкyжсгвВрЧвдкЖдГЦжсзѓВрКЭгвВрШ§жжЧщПіЬжТлЃЌжБНгЧѓГізюИпЕугызюЕЭЕуЕФзнзјБъжЎВюМДПЩЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЬжТлЃЌЕБmЃМ0ЃЌХзЮяЯпОЙ§ЯпЖЮЕФзюзѓЖЫЕу![]() ЪБЃЌЧѓГіmЕФжЕВЂЛГіЭМЯѓМДПЩгЩЭМЯѓПДГіmЕФШЁжЕЗЖЮЇЃЛЕБmЁн0ЃЌХзЮяЯпОЙ§ЯпЖЮЕФзюгвЖЫЕуB
ЪБЃЌЧѓГіmЕФжЕВЂЛГіЭМЯѓМДПЩгЩЭМЯѓПДГіmЕФШЁжЕЗЖЮЇЃЛЕБmЁн0ЃЌХзЮяЯпОЙ§ЯпЖЮЕФзюгвЖЫЕуB![]() ЪБЃЌЧѓГіmЕФжЕВЂЛГіЭМЯѓМДПЩгЩЭМЯѓПДГіmЕФШЁжЕЗЖЮЇЃЎ
ЪБЃЌЧѓГіmЕФжЕВЂЛГіЭМЯѓМДПЩгЩЭМЯѓПДГіmЕФШЁжЕЗЖЮЇЃЎ
ЃЈ1ЃЉyЃНx2Љ2mx+m2Љ2
ЃНЃЈxЉmЃЉ2Љ2ЃЌ
ЁрЖЅЕузјБъЮЊЃЈmЃЌЉ2ЃЉЃЌ
дкyЃНx2Љ2mx+m2Љ2жаЃЌ
ЕБxЃН0ЪБЃЌyЃНm2Љ2ЃЌ
ЁрЕуCзјБъЮЊЃЈ0ЃЌm2Љ2ЃЉЃЌ
ЙЪД№АИЮЊЃКЃЈmЃЌЉ2ЃЉЃЌЃЈ0ЃЌm2Љ2ЃЉЃЛ
ЃЈ2ЃЉЂйЕБmЃН1ЪБЃЌyЃНx2Љ2xЉ1ЃЌ
ЁрPЃЈnЃЌn2Љ2nЉ2ЃЉЃЌ
Сюn2Љ2nЉ1ЃНЉ2ЃЌ
НтЕУЃЌn1ЃНn2ЃН1ЃЌ
ЁрP1ЃЈ1ЃЌЉ2ЃЉЃЛ
Сюn2Љ2nЉ1ЃН2ЃЌ
НтЕУЃЌn1ЃН3ЃЌn2ЃНЉ1ЃЈnЃО0ЃЌЩсШЅЃЉЃЌ
ЁрP2ЃЈ3ЃЌ2ЃЉЃЌ
злЩЯЃКP1ЃЈ1ЃЌЉ2ЃЉЃЌP2ЃЈ3ЃЌ2ЃЉЃЛ
ЂкдкyЃНx2Љ2xЉ1жаЃЌЖдГЦжсЮЊ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
ЁрЖЅЕузјБъЮЊ![]() ЃЌ
ЃЌ
ЁпЕуPЕФКсзјБъЮЊnЃЌ
ЁрЕуPЕФКсзјБъЮЊ![]() ЃЌ
ЃЌ
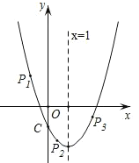
ШчЭМЃЌЕБЕуPдкyжсзѓВрЃЌМД![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЛ
ЃЛ
ЕБдкyжсгвВрЧвдкЖдГЦжсзѓВрЃЌМД![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЛ
ЃЛ
ЕБдкЖдГЦжсгвВрЃЌМД![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЛ
ЃЛ
злЩЯЃК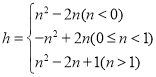
ЃЈ3ЃЉЂйЕБmЃМ0ЃЌХзЮяЯпОЙ§ЯпЖЮЕФзюзѓЖЫЕуAЃЈЉ3ЃЌ2ЃЉЪБЃЌ
ЃЈЉ3ЉmЃЉ2Љ2ЃН2ЃЌ
НтЕУЃЌm1ЃНЉ5ЃЌm2ЃНЉ1ЃЌ
ЁрЖдгІХзЮяЯпЕФЭМЯѓШчЭМ1ЃЌЭМ2ЫљЪОЃЌ

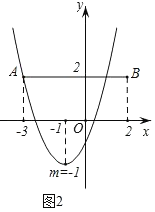
гЩЭМЯѓПЩвдПДГіЕБЉ5ЁмmЃМЉ1ЪБЃЌХзЮяЯпyЃНx2Љ2mx+m2Љ2гыЯпЖЮABжЛгавЛИіНЛЕуЃЛ
ЂкЕБmЁн0ЃЌХзЮяЯпОЙ§ЯпЖЮЕФзюгвЖЫЕуBЃЈ2ЃЌ2ЃЉЪБЃЌ
ЃЈ2ЉmЃЉ2Љ2ЃН2ЃЌ
НтЕУЃЌm1ЃН4ЃЌm2ЃН0ЃЌ
ЁрЖдгІХзЮяЯпЕФЭМЯѓШчЭМ3ЃЌЭМ4ЫљЪОЃЌ

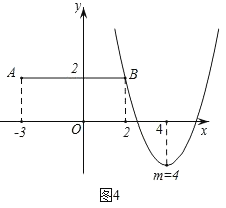
гЩЭМЯѓПЩвдПДГіЕБ0ЃМmЁм4ЪБЃЌХзЮяЯпyЃНx2Љ2mx+m2Љ2гыЯпЖЮABжЛгавЛИіНЛЕуЃЛ
злЩЯЫљЪіЃКmЕФШЁжЕЗЖЮЇЮЊЉ5ЁмmЃМЉ1Лђ0ЃМmЁм4ЃЎ


 ОйвЛЗДШ§ЭЌВНЧЩНВОЋСЗЯЕСаД№АИ
ОйвЛЗДШ§ЭЌВНЧЩНВОЋСЗЯЕСаД№АИ ПкЫугыгІгУЬтПЈЯЕСаД№АИ
ПкЫугыгІгУЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
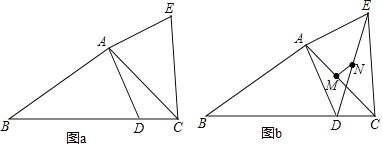
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯACBЃН45ЁуЃЌBCЃН5ЃЌACЃН2![]() ЃЌDЪЧBCБпЩЯЕФЖЏЕуЃЌСЌНгADЃЌНЋЯпЖЮADШЦЕуAФцЪБеыа§зЊ90ЁуЕУЕНЯпЖЮAEЃЌСЌНгECЃЎ
ЃЌDЪЧBCБпЩЯЕФЖЏЕуЃЌСЌНгADЃЌНЋЯпЖЮADШЦЕуAФцЪБеыа§зЊ90ЁуЕУЕНЯпЖЮAEЃЌСЌНгECЃЎ
ЃЈ1ЃЉШчЭМaЃЌЧѓжЄЃКCEЁЭBCЃЛ
ЃЈ2ЃЉСЌНгEDЃЌMЮЊACЕФжаЕуЃЌNЮЊEDЕФжаЕуЃЌСЌНгMNЃЌШчЭМbЃЎ
ЂйаДГіDEЁЂACЃЌMNШ§ЬѕЯпЖЮЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЂкдкЕуDдЫЖЏЕФЙ§ГЬжаЃЌЕБBDЕФГЄЮЊКЮжЕЪБЃЌMЃЌEСНЕужЎМфЕФОрРызюаЁЃПзюаЁжЕЪЧЁЁ ЁЁЃЌЧыжБНгаДГіНсЙћЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкxЕФвЛдЊЖўДЮЗНГЬx2+3x+m-1=0ЕФСНИіЪЕЪ§ИљЗжБ№ЮЊx1,x2ЃЎ
ЃЈ1ЃЉЧѓmЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉШє2ЃЈx1+x2ЃЉ+ x1x2+10=0ЃЎЧѓmЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛИіЖўДЮКЏЪ§ЭМЯѓЩЯВПЗжЕуЕФКсзјБъ![]() гызнзјБъ
гызнзјБъ![]() ЕФЖдгІжЕШчЯТБэЫљЪОЃК
ЕФЖдгІжЕШчЯТБэЫљЪОЃК
| ... |
|
|
|
|
| ... |
| ... |
|
|
|
|
| ... |
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉдкИјЖЈЕФЦНУцжБНЧзјБъЯЕжаЛГіетИіЖўДЮКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ3![]() ЪБЃЌ
ЪБЃЌ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌОиаЮABCDЕФБпAB:BCЃН3:2ЃЌЕуAЃЈ3ЃЌ0ЃЉЃЌBЃЈ0ЃЌ6ЃЉЗжБ№дкxжсЃЌyжсЩЯЃЌЗДБШР§КЏЪ§![]() (xЃО0)ЕФЭМЯёОЙ§ЕуDЃЌдђ
(xЃО0)ЕФЭМЯёОЙ§ЕуDЃЌдђ![]() жЕЮЊЃЈ ЃЉ
жЕЮЊЃЈ ЃЉ
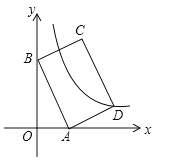
A. Љ14 B. 14 C. 7 D. Љ7
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() ЃЌyЪЧЙигк
ЃЌyЪЧЙигк![]() ЕФЖўДЮКЏЪ§ЃЌХзЮяЯп
ЕФЖўДЮКЏЪ§ЃЌХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() .ХзЮяЯп
.ХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() ХзЮяЯп
ХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() ХзЮяЯп
ХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() дђЯТСаХаЖЯЃК
дђЯТСаХаЖЯЃК
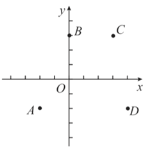
ЂйЫФЬѕХзЮяЯпЕФПЊПкЗНЯђОљЯђЯТЃЛ
ЂкЕБ![]() ЪБЃЌЫФЬѕХзЮяЯпБэДяЪНжаЕФ
ЪБЃЌЫФЬѕХзЮяЯпБэДяЪНжаЕФ![]() ОљЫц
ОљЫц![]() ЕФдіДѓЖјдіДѓЃЛ
ЕФдіДѓЖјдіДѓЃЛ
ЂлХзЮяЯп![]() ЕФЖЅЕудкХзЮяЯп
ЕФЖЅЕудкХзЮяЯп![]() ЖЅЕуЕФЩЯЗНЃЛ
ЖЅЕуЕФЩЯЗНЃЛ
ЂмХзЮяЯп![]() гы
гы![]() жсНЛЕудкЕу
жсНЛЕудкЕу![]() ЕФЩЯЗН.
ЕФЩЯЗН.
Цфжае§ШЗЕФЪЧ
A.ЂйЂкЂмB.ЂйЂлЂм
C.ЂйЂкЂлD.ЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
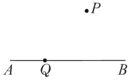
ЁОЬтФПЁПШчЭМЃЌдкЦНУцФкЁЃЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯШЮвтвЛЕу.ЖдгкИУЦНУцФкШЮвтЕФЕу
ЩЯШЮвтвЛЕу.ЖдгкИУЦНУцФкШЮвтЕФЕу![]() ЃЌШєТњзу
ЃЌШєТњзу![]() аЁгкЕШгк
аЁгкЕШгк![]() дђГЦЕу
дђГЦЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФЁАЯоОрЕуЁБ.
ЕФЁАЯоОрЕуЁБ.
ЃЈ1ЃЉдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌШєЕу
жаЃЌШєЕу![]() .
.
ЂйдкЕФЕу![]() жаЃЌЪЧЯпЖЮ
жаЃЌЪЧЯпЖЮ![]() ЕФЁАЯоОрЕуЁБЕФЪЧ ЃЛ
ЕФЁАЯоОрЕуЁБЕФЪЧ ЃЛ
ЂкЕуPЪЧжБЯп![]() ЩЯвЛЕуЃЌШєЕуPЪЧЯпЖЮABЕФЁАЯоОрЕуЁБЃЌЧыЧѓГіЕуPКсзјБъ
ЩЯвЛЕуЃЌШєЕуPЪЧЯпЖЮABЕФЁАЯоОрЕуЁБЃЌЧыЧѓГіЕуPКсзјБъ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ЃЈ2ЃЉдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌШєЕу
жаЃЌШєЕу![]() .ШєжБЯп
.ШєжБЯп![]() ЩЯДцдкЯпЖЮABЕФЁАЯоОрЕуЁБЃЌЧыжБНгаДГі
ЩЯДцдкЯпЖЮABЕФЁАЯоОрЕуЁБЃЌЧыжБНгаДГі![]() ЕФШЁжЕЗЖЮЇ
ЕФШЁжЕЗЖЮЇ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
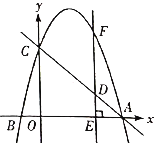
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() .
.
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪН.
ЃЈ2ЃЉЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯвЛЖЏЕуЃЌЙ§Еу
ЩЯвЛЖЏЕуЃЌЙ§Еу![]() зї
зї![]() ДЙжБгк
ДЙжБгк![]() жсгкЕу
жсгкЕу![]() ЃЌНЛХзЮяЯпгкЕу
ЃЌНЛХзЮяЯпгкЕу![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ЕФГЄЖШзюДѓжЕ.
ЕФГЄЖШзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЙигкxЕФЗНГЬЃЈxЉ4ЃЉЃЈx2Љ6x+mЃЉЃН0ЕФШ§ИіИљЧЁКУПЩвдзщГЩФГжБНЧШ§НЧаЮЕФШ§БпГЄЃЌдђmЕФжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com