
有四个实验:
(1)从黑、蓝、红三支颜色的笔和白、绿两块橡皮中任意拿一只笔和一块橡皮,考查取到红笔、绿橡皮的机会为多少?
(2)从一副去掉大小王的52张牌中,抽到方块的机会是多少?
(3)在1~10中任取两个数的和为奇数的机会是多少?
(4)如图是一些卡片,它们的背面都一样,现将它们背面朝上,从中任意摸一纸片,则摸到奇数卡的机会是多少?
请在四个实验中选取两个进行模拟实验,自己设计模拟实验的方案.
科目:初中数学 来源: 题型:
 方形面上的概率为
方形面上的概率为| 1 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
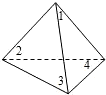
 (一)如图,放在直角坐标系中的正方形ABCD的边长为4.现做如下实验:
(一)如图,放在直角坐标系中的正方形ABCD的边长为4.现做如下实验:| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
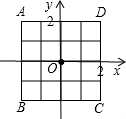 如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).
如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《图形的平移》(01)(解析版) 题型:解答题
 ?若存在,指出其中的一种平移方式;若不存在,请说明理由;
?若存在,指出其中的一种平移方式;若不存在,请说明理由;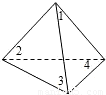
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com