
ЁОЬтФПЁПШчЭМ1ЃЌ![]() ЕФгрЧажЕЮЊ2ЃЌ
ЕФгрЧажЕЮЊ2ЃЌ![]() ЃЌЕуDЪЧЯпЖЮ
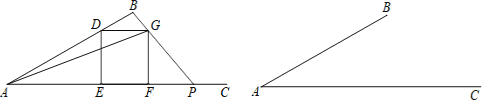
ЃЌЕуDЪЧЯпЖЮ![]() ЩЯЕФвЛЖЏЕуЃЈЕуDВЛгыЕуAЁЂBжиКЯЃЉЃЌвдЕуDЮЊЖЅЕуЕФе§ЗНаЮ
ЩЯЕФвЛЖЏЕуЃЈЕуDВЛгыЕуAЁЂBжиКЯЃЉЃЌвдЕуDЮЊЖЅЕуЕФе§ЗНаЮ![]() ЕФСэСНИіЖЅЕуEЁЂFЖМдкЩфЯп
ЕФСэСНИіЖЅЕуEЁЂFЖМдкЩфЯп![]() ЩЯЃЌЧвЕуFдкЕуEЕФгвВрЃЌСЊНс
ЩЯЃЌЧвЕуFдкЕуEЕФгвВрЃЌСЊНс![]() ЃЌВЂбгГЄ
ЃЌВЂбгГЄ![]() ЃЌНЛЩфЯп
ЃЌНЛЩфЯп![]() гкЕуPЃЎ
гкЕуPЃЎ
ЃЈ1ЃЉЕуDдкдЫЖЏЪБЃЌЯТСаЕФЯпЖЮКЭНЧжаЃЌ________ЪЧЪМжеБЃГжВЛБфЕФСПЃЈЬюађКХЃЉЃЛ
Ђй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЛЂн
ЃЛЂн![]() ЃЛЂо
ЃЛЂо![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩше§ЗНаЮЕФБпГЄЮЊxЃЌЯпЖЮ![]() ЕФГЄЮЊyЃЌЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЖЈвхгђЃЛ
ЕФГЄЮЊyЃЌЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЖЈвхгђЃЛ
ЃЈ3ЃЉШчЙћ![]() гы
гы![]() ЯрЫЦЃЌЕЋУцЛ§ВЛЯрЕШЃЌЧѓДЫЪБе§ЗНаЮЕФБпГЄЃЎ
ЯрЫЦЃЌЕЋУцЛ§ВЛЯрЕШЃЌЧѓДЫЪБе§ЗНаЮЕФБпГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂмЂнЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉзї![]() гкMЃЌНЛ
гкMЃЌНЛ![]() гкNЃЌШчЭМЃЌРћгУШ§НЧКЏЪ§ЕФЖЈвхЕУЕН
гкNЃЌШчЭМЃЌРћгУШ§НЧКЏЪ§ЕФЖЈвхЕУЕН![]() ЃЌЩш
ЃЌЩш![]() ЃЌдђ
ЃЌдђ![]() ЃЌРћгУЙДЙЩЖЈРэЕУ
ЃЌРћгУЙДЙЩЖЈРэЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ![]() ЃЌЩше§ЗНаЮЕФБпГЄЮЊxЃЌдђ
ЃЌЩше§ЗНаЮЕФБпГЄЮЊxЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌгЩгк
ЃЌгЩгк![]() ЃЌдђПЩХаЖЯ
ЃЌдђПЩХаЖЯ![]() ЮЊЖЈжЕЃЛдйРћгУ
ЮЊЖЈжЕЃЛдйРћгУ![]() ЕУЕН
ЕУЕН![]() ЃЌдђПЩХаЖЯ
ЃЌдђПЩХаЖЯ![]() ЮЊЖЈжЕЃЛдк
ЮЊЖЈжЕЃЛдк![]() жаЃЌРћгУЙДЙЩЖЈРэКЭШ§НЧКЏЪ§ПЩХаЖЯ
жаЃЌРћгУЙДЙЩЖЈРэКЭШ§НЧКЏЪ§ПЩХаЖЯ![]() дкБфЛЏЃЌ
дкБфЛЏЃЌ![]() дкБфЛЏЃЌ
дкБфЛЏЃЌ![]() дкБфЛЏЃЛ
дкБфЛЏЃЛ
ЃЈ2ЃЉвзЕУЫФБпаЮ![]() ЮЊОиаЮЃЌдђ
ЮЊОиаЮЃЌдђ![]() ЃЌжЄУї
ЃЌжЄУї![]() ЃЌРћгУЯрЫЦБШПЩЕУЕНyгыxЕФЙиЯЕЪНЃЛ
ЃЌРћгУЯрЫЦБШПЩЕУЕНyгыxЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉгЩгк![]() ЃЌ
ЃЌ![]() гы
гы![]() ЯрЫЦЃЌЧвУцЛ§ВЛЯрЕШЃЌРћгУЯрЫЦБШЕУЕН
ЯрЫЦЃЌЧвУцЛ§ВЛЯрЕШЃЌРћгУЯрЫЦБШЕУЕН![]() ЃЌЬжТлЃКЕБЕуPдкЕуFЕугвВрЪБЃЌдђ
ЃЌЬжТлЃКЕБЕуPдкЕуFЕугвВрЪБЃЌдђ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌЕБЕуPдкЕуFЕузѓВрЪБЃЌдђ
ЃЌЕБЕуPдкЕуFЕузѓВрЪБЃЌдђ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌШЛКѓЗжБ№НтЗНГЬМДПЩЕУЕНе§ЗНаЮЕФБпГЄЃЎ
ЃЌШЛКѓЗжБ№НтЗНГЬМДПЩЕУЕНе§ЗНаЮЕФБпГЄЃЎ
ЃЈ1ЃЉШчЭМЃЌзї![]() гкMЃЌНЛ
гкMЃЌНЛ![]() гкNЃЌ
гкNЃЌ
дк![]() жаЃЌЁп
жаЃЌЁп![]() ЃЌ
ЃЌ
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Щше§ЗНаЮЕФБпГЄЮЊxЃЌ
дк![]() жаЃЌЁп
жаЃЌЁп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЮЊЖЈжЕЃЛ
ЮЊЖЈжЕЃЛ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЮЊЖЈжЕЃЛ
ЮЊЖЈжЕЃЛ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
Жј![]() дкБфЛЏЃЌ
дкБфЛЏЃЌ
Ёр![]() дкБфЛЏЃЌ
дкБфЛЏЃЌ![]() дкБфЛЏЃЌ
дкБфЛЏЃЌ
Ёр![]() дкБфЛЏЃЌ
дкБфЛЏЃЌ
Ыљвд![]() КЭ
КЭ![]() ЪЧЪМжеБЃГжВЛБфЕФСПЃЛ
ЪЧЪМжеБЃГжВЛБфЕФСПЃЛ

ЙЪД№АИЮЊЃКЂмЂн
ЃЈ2ЃЉЁпMNЁЭAPЃЌDEFGЪЧе§ЗНаЮЃЌ
ЁрЫФБпаЮ![]() ЮЊОиаЮЃЌ
ЮЊОиаЮЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
Ёр![]()
ЃЈ3ЃЉЁп![]() ЃЌ
ЃЌ![]() гы
гы![]() ЯрЫЦЃЌЧвУцЛ§ВЛЯрЕШЃЌ
ЯрЫЦЃЌЧвУцЛ§ВЛЯрЕШЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЕБЕуPдкЕуFЕугвВрЪБЃЌAP=AF+PF=![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЕБЕуPдкЕуFЕузѓВрЪБЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ

злЩЯЫљЪіЃЌе§ЗНаЮЕФБпГЄЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ


 ЛЦИдЙкОќПЮПЮСЗЯЕСаД№АИ
ЛЦИдЙкОќПЮПЮСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП ШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФЖЅЕуOдкзјБъдЕуЃЌБпOAдкxжсЩЯЃЌ
OCдкyжсЩЯЃЌШчЙћОиаЮOAЁфBЁфCЁфгыОиаЮOABCЙигкЕуOЮЛЫЦЃЌЧвОиаЮOAЁфBЁфCЁфЕФУцЛ§ЕШгкОиаЮOABCУцЛ§ЕФ![]() ЃЌФЧУДЕуBЁфЕФзјБъЪЧЁО ЁП
ЃЌФЧУДЕуBЁфЕФзјБъЪЧЁО ЁП
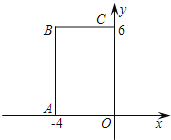
AЃЎЃЈЃ2ЃЌ3ЃЉ BЃЎЃЈ2ЃЌЃ3ЃЉ CЃЎЃЈ3ЃЌЃ2ЃЉЛђЃЈЃ2ЃЌ3ЃЉ DЃЎЃЈЃ2ЃЌ3ЃЉЛђЃЈ2ЃЌЃ3ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЗсИЛаЃдАЮФЛЏЩњЛюЃЌЬсИпбЇЩњЕФзлКЯЫижЪЃЌДйНјжабЇЩњШЋУцЗЂеЙЃЌбЇаЃПЊеЙСЫЖржжЩчЭХЛюЖЏЃЎаЁУїЯВЛЖЕФЩчЭХгаЃККЯГЊЩчЭХЁЂзуЧђЩчЭХЁЂЪщЗЈЩчЭХЁЂПЦММЩчЭХЃЈЗжБ№гУзжФИAЃЌBЃЌCЃЌDвРДЮБэЪОетЫФИіЩчЭХЃЉЃЌВЂАбетЫФИізжФИЗжБ№аДдкЫФеХЭъШЋЯрЭЌЕФВЛЭИУїЕФПЈЦЌЕФе§УцЩЯЃЌШЛКѓНЋетЫФеХПЈЦЌБГУцГЏЩЯЯДдШКѓЗХдкзРУцЩЯЃЎ
ЃЈ1ЃЉаЁУїДгжаЫцЛњГщШЁвЛеХПЈЦЌЪЧзуЧђЩчЭХBЕФИХТЪЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉаЁУїЯШДгжаЫцЛњГщШЁвЛеХПЈЦЌЃЌМЧТМЯТПЈЦЌЩЯЕФзжФИКѓВЛЗХЛиЃЌдйДгЪЃгрЕФПЈЦЌжаЫцЛњГщШЁвЛеХПЈЦЌЃЌМЧТМЯТПЈЦЌЩЯЕФзжФИЃЎЧыФугУСаБэЗЈЛђЛЪїзДЭМЗЈЧѓГіаЁУїСНДЮГщШЁЕФПЈЦЌжагавЛеХЪЧПЦММЩчЭХDЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПТІЕзЪаФГТЅХЬзМБИвдУПЦНЗНУз5000дЊЕФОљМлЖдЭтЯњЪлЃЌгЩгкЙњЮёдКгаЙиЗПЕиВњЕФаТеўВпГіЬЈКѓЃЌЙКЗПепГжБвЙлЭћ.ЮЊСЫМгПьзЪН№жмзЊЃЌЗПЕиВњПЊЗЂЩЬЖдМлИёОЙ§СНДЮЯТЕїКѓЃЌОіЖЈвдУПЦНЗНУз4050дЊЕФОљМлПЊХЬЯњЪл.
(1)ЧѓЦНОљУПДЮЯТЕїЕФАйЗжТЪЃЛ
(2)ФГШЫзМБИвдПЊХЬОљМлЙКТђвЛЬз150ЦНЗНУзЕФЗПзг.ПЊЗЂЩЬЛЙИјгшвдЯТСНжжгХЛнЗНАИвдЙЉбЁдёЃКЂйДђ9.8елЯњЪлЃЛЂкВЛДђелЃЌЫЭШ§ФъЮявЕЙмРэЗб.ЮявЕЙмРэЗбЮЊУПЦНЗНУзУПдТ1.5дЊ.ЧыЮЪФФжжЗНАИИќгХЛнЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
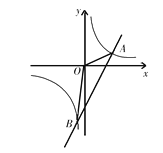
ЁОЬтФПЁПШчЭМЃЌжБЯпy1=3xЉ5гыЗДБШР§КЏЪ§y2=![]() ЕФЭМЯѓЯрНЛAЃЈ2ЃЌmЃЉЃЌBЃЈnЃЌЉ6ЃЉСНЕуЃЌСЌНгOAЃЌOBЃЎ
ЕФЭМЯѓЯрНЛAЃЈ2ЃЌmЃЉЃЌBЃЈnЃЌЉ6ЃЉСНЕуЃЌСЌНгOAЃЌOBЃЎ
ЃЈ1ЃЉЧѓkКЭnЕФжЕЃЛ
ЃЈ2ЃЉЧѓЁїAOBЕФУцЛ§ЃЛ
ЃЈ3ЃЉжБНгаДГіy1ЃО y2ЪБздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌжБЯпy=kx+3гы
жаЃЌжБЯпy=kx+3гы![]() жсЁЂ
жсЁЂ![]() жсЗжБ№ЯрНЛгкЕуAЁЂBЃЌВЂгыХзЮяЯп
жсЗжБ№ЯрНЛгкЕуAЁЂBЃЌВЂгыХзЮяЯп![]() ЕФЖдГЦжсНЛгкЕу
ЕФЖдГЦжсНЛгкЕу![]() ЃЌХзЮяЯпЕФЖЅЕуЪЧЕу
ЃЌХзЮяЯпЕФЖЅЕуЪЧЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓkКЭbЕФжЕЃЛ
ЃЈ2ЃЉЕуGЪЧ![]() жсЩЯвЛЕуЃЌЧввдЕу
жсЩЯвЛЕуЃЌЧввдЕу![]() ЁЂCЁЂ
ЁЂCЁЂ![]() ЮЊЖЅЕуЕФШ§НЧаЮгыЁї
ЮЊЖЅЕуЕФШ§НЧаЮгыЁї![]() ЯрЫЦЃЌЧѓЕуGЕФзјБъЃЛ
ЯрЫЦЃЌЧѓЕуGЕФзјБъЃЛ
ЃЈ3ЃЉдкХзЮяЯпЩЯЪЧЗёДцдкЕуEЃКЫќЙигкжБЯпABЕФЖдГЦЕуFЧЁКУдкyжсЩЯЃЎШчЙћДцдкЃЌжБНгаДГіЕуEЕФзјБъЃЌШчЙћВЛДцдкЃЌЪдЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
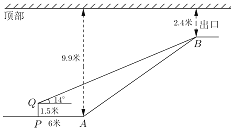
ЁОЬтФПЁПЕиЬњ10КХЯпФГеОЕуГіПкКсНиУцЦНУцЭМШчЭМЫљЪОЃЌЕчЬн![]() ЕФСНЖЫЗжБ№ОрЖЅВП9.9УзКЭ2.4УзЃЌдкОрЕчЬнЦ№Еу
ЕФСНЖЫЗжБ№ОрЖЅВП9.9УзКЭ2.4УзЃЌдкОрЕчЬнЦ№Еу![]() ЖЫ6УзЕФ
ЖЫ6УзЕФ![]() ДІЃЌгУ1.5УзЕФВтНЧвЧВтЕУЕчЬнжеЖЫ
ДІЃЌгУ1.5УзЕФВтНЧвЧВтЕУЕчЬнжеЖЫ![]() ДІЕФбіНЧЮЊ14ЁуЃЌЧѓЕчЬн
ДІЕФбіНЧЮЊ14ЁуЃЌЧѓЕчЬн![]() ЕФЦТЖШгыГЄЖШ.ЃЈВЮПМЪ§ОнЃК
ЕФЦТЖШгыГЄЖШ.ЃЈВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌЯв
ЕФжБОЖЃЌЯв![]() ЃЌ
ЃЌ![]()
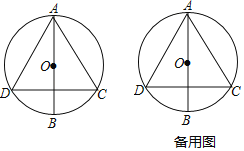
ЃЈ1ЃЉЧѓжЄЃК![]() ЪЧЕШБпШ§НЧаЮЃЎ
ЪЧЕШБпШ§НЧаЮЃЎ
ЃЈ2ЃЉШєЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌШє
ЃЌШє![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ3ЃЉШє![]() ЕФАыОЖЮЊ4ЃЌЕу
ЕФАыОЖЮЊ4ЃЌЕу![]() ЪЧЯв
ЪЧЯв![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЕФШЮвтвЛЕуЃЌНЋЕу
ЩЯЕФШЮвтвЛЕуЃЌНЋЕу![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ60ЁуЕУЕу
ФцЪБеыа§зЊ60ЁуЕУЕу![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпyЃНax2Љx+cЕФЖдГЦжсЮЊжБЯпxЃН1ЃЌгыxжсЕФвЛИіНЛЕуЮЊAЃЈЉ1ЃЌ0ЃЉЃЌЖЅЕуЮЊBЃЎЕуCЃЈ5ЃЌmЃЉдкХзЮяЯпЩЯЃЌжБЯпBCНЛxжсгкЕуEЃЎ
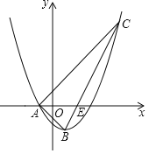
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНМАЕуEЕФзјБъЃЛ
ЃЈ2ЃЉСЊНсABЃЌЧѓЁЯBЕФе§ЧажЕЃЛ
ЃЈ3ЃЉЕуGЮЊЯпЖЮACЩЯвЛЕуЃЌЙ§ЕуGзїCBЕФДЙЯпНЛxжсгкЕуMЃЈЮЛгкЕуEгвВрЃЉЃЌЕБЁїCGMгыЁїABEЯрЫЦЪБЃЌЧѓЕуMЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com