
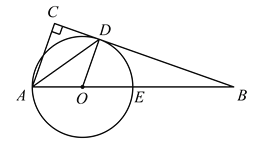
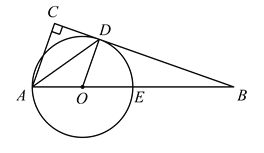
【题目】如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,点O是AB边上一点,以O为圆心作⊙O且经过A,D两点,交AB于点E.
(1)求证:BC是⊙O的切线;
(2)AC=2,AB=6,求BE的长.
【答案】(1)证明见解析;(2)3.
【解析】试题分析:(1)连接OD,根据角平分线的定义和等腰三角形的性质证明OD∥AC,根据平行线的性质得到∠BOD=90°,根据切线的判定定理证明;
(2)由OD∥AC可证△BDO∽△BCA,由相似三角形的性质得![]() .设OD=r,则BO=6﹣r,代入比例式求出r,从而求出BE的值.
.设OD=r,则BO=6﹣r,代入比例式求出r,从而求出BE的值.
(1)证明:连结OD,∵OA=OD,∴∠OAD=∠ODA.
∵AD平分∠BAC,∴∠CAD=∠OAD,∴∠CAD=∠ODA,∴OD∥AC.
∵∠ACB=90°,∴∠ODB=90°.
即OD⊥BC于D,∴BC是⊙O的切线.
(2)∵OD∥AC,∴△BDO∽△BCA,∴ ![]() .
.
∵AC=2,AB=6,∴设OD=r,则BO=6﹣r,∴ ![]() .
.
解得r=![]() ,∴AE=3,∴BE=3.
,∴AE=3,∴BE=3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小明为了检验两枚六个面分别刻有点数1、 2、3、4、5、6的正六面体骰子的质量是否都合格,在相同的条件下,同时抛两枚骰子20 00 0次,结果发现两个朝上面的点数和是7的次数为20次.你认为这两枚骰子质量是否都合格(合格标准为:在相同条件下抛骰子时,骰子各个面朝上的机会相等)?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:正方形折叠中的数学
已知正方形纸片ABCD中,AB=4,点E是AB边上的一点,点G是CE的中点,将正方形纸片沿CE所在直线折叠,点B的对应点为点B′.
(1)如图1,当∠BCE=30°时,连接BG,B′G,求证:四边形BEB′G是菱形;
深入探究:
(2)在CD边上取点F,使DF=BE,点H是AF的中点,再将正方形纸片ABCD沿AF所在直线折叠,点D的对应点为D′,顺次连接B′,G,D′,H,B',得到四边形B′GD′H.
请你从A,B两题中任选一题作答,我选择 题.
A题:如图2,当点B',D′均落在对角线AC上时,
①判断B′G与D′H的数量关系与位置关系,并说明理由;
②直写出此时点H,G之间的距离.
B题:如图3,点M是AB的中点,MN∥BC交CD于点N,当点B',D′均落在MN上时,
①判断B′G与D′H的数量关系与位置关系,并说明理由;
②直接写出此时点H,G之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
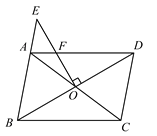
【题目】如图,在□ABCD中,对角线AC,BD交于点O,过点O作EO⊥BD,交BA延长线于点E,交AD于点F,若EF=OF,∠CBD=30°,BD=![]() .求AF的长.
.求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
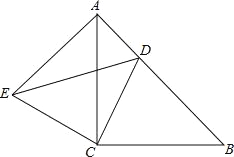
【题目】如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,
(1)求证:△ACE≌△BCD;
(2)若DE=13,BD=12,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com