
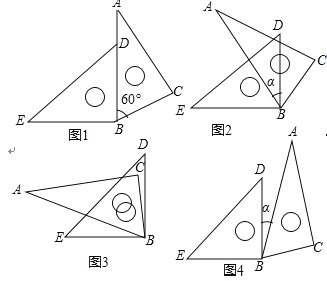
【题目】图1是由一副三角板拼成的图案,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求图1中![]() 的度数;
的度数;
(2)若将图1中的三角板![]() 不动,将另一三角板
不动,将另一三角板![]() 绕点
绕点![]() 顺时针或逆时针旋转
顺时针或逆时针旋转![]() 度(
度(![]() ).当
).当![]() 时,求
时,求![]() 的度数(图2,图3,图4仅供参考).
的度数(图2,图3,图4仅供参考).
【答案】(1)150°;(2)30°或70°
【解析】
(1)∠EBC是由一个直角和一个60°的角组成的;
(2)分不同方向旋转,求得α,等量关系为∠ABE=2∠DBC,应用α表示出这个等量关系,进而求解.
(1)∠EBC=∠ABC+∠EBD=60°+90°=150°.
(2)①第一种情况:
若逆时针旋转α度(0<α<60°),如图2:

据题意得90°-α=2(60°-α),
得α=30°,
∴∠EBC=90°+(60°-30°)=120°,
∴∠DBC=120°-90°=30°,
∴∠ABD=60°-30°=30°;
第二种情况,若逆时针旋转α度(60°≤α<90°),
据题意得90°-α=2(α-60°),
得α=70°,
∴∠EBC=90°-(70°-60°)=80°,
∴∠DBC=90°-80°=10°,
∵∠ABD=60°+10°=70°;
第三种情况:若顺时针旋转α度,如图3,

据题意得90°+α=2(60°+α),
得α=-30°
∵0<α<90°,α=-30°不合题意,舍去,
故∠ABD=30°或70°.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-4x-m2=0
(1)求证:该方程有两个不等的实根;
(2)若该方程的两实根x1、x2满足x1+2x2=9,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如构造图1可以得到![]() .请解答下列问题:
.请解答下列问题:
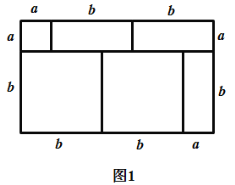
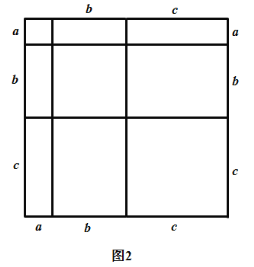
(1)仿照图1,构造适当的图形得到![]() 的值;
的值;
(2)写出图2中所表示的数学等式;
(3)利用(2)中所得到的结论,解决下面的问题:己知![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列结论中错误的是( )
A.△BDF∽△BEC
B.△BFA∽△BEC
C.△BAC∽△BDA
D.△BDF∽△BAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,点
,点![]() 是射线
是射线![]() 上一动点(与点
上一动点(与点![]() 不重合),
不重合),![]() 分别平分
分别平分![]() 和
和![]() ,分别交射线
,分别交射线![]() 于点
于点![]()
![]()
![]() 若点
若点![]() 运动到某处时,恰有
运动到某处时,恰有![]() ,此时
,此时![]() 与
与![]() 有何位置关系?请说明理由.
有何位置关系?请说明理由.
![]() 在点
在点![]() 运动的过程中,
运动的过程中,![]() 与
与![]() 之间的关系是否发生变化?若不变,请写出它们的关系并说明理由;若变化,请写出变化规律.
之间的关系是否发生变化?若不变,请写出它们的关系并说明理由;若变化,请写出变化规律.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为6![]() 米,山坡的坡角为30°. 小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF = 1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°(结果精确到0.1).
米,山坡的坡角为30°. 小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF = 1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°(结果精确到0.1).
(1)求树AB与测角仪EF的水平距离DF的长;
(2)求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36, ![]() ≈1.73 )
≈1.73 )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com