
【题目】如图①,![]() 的顶点
的顶点![]() 在正方形
在正方形![]() 两条对角线的交点处,
两条对角线的交点处,![]() ,将
,将![]() 绕点
绕点![]() 旋转,旋转过程中
旋转,旋转过程中![]() 的两边分别与正方形
的两边分别与正方形![]() 的边
的边![]() 和
和![]() 交于点
交于点![]() 和点
和点![]() (点
(点![]() 与点
与点![]() ,
,![]() 不重合).
不重合).
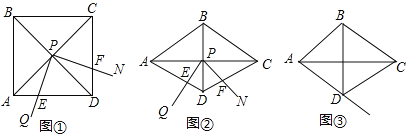
(1)如图①,当![]() 时,求
时,求![]() ,
,![]() ,
,![]() 之间满足的数量关系,并证明;
之间满足的数量关系,并证明;
(2)如图②,将图①中的正方形![]() 改为
改为![]() 的菱形,其他条件不变,当
的菱形,其他条件不变,当![]() 时,(1)中的结论变为
时,(1)中的结论变为![]() ,请给出证明;
,请给出证明;
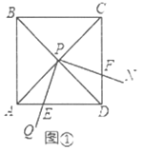
(3)在(2)的条件下,若旋转过程中![]() 的边
的边![]() 与射线
与射线![]() 交于点
交于点![]() ,其他条件不变,探究在整个运动变化过程中,
,其他条件不变,探究在整个运动变化过程中,![]() ,
,![]() ,
,![]() 之间满足的数量关系,直接写出结论,不用加以证明.
之间满足的数量关系,直接写出结论,不用加以证明.
【答案】(1)![]() ;(2)见解析;(3)当点
;(2)见解析;(3)当点![]() 落在
落在![]() 上时
上时![]() ,当点
,当点![]() 落在
落在![]() 的延长线上时DF-DE=
的延长线上时DF-DE=![]() AD,见解析.
AD,见解析.
【解析】
(1)利用正方形的性质得出角与线段的关系,易证得△APE≌△DPF,可得出AE=DF,即可得出结论DE+DF=AD,
(2)取AD的中点M,连接PM,利用菱形的性质,可得出△MDP是等边三角形,易证△MPE≌△FPD,得出ME=DF,由DE+ME=![]() AD,即可得出DE+DF=
AD,即可得出DE+DF=![]() AD,
AD,
(3))①当点E落在AD上时,DE+DF=![]() AD,②当点E落在AD的延长线上时,DF-DE=
AD,②当点E落在AD的延长线上时,DF-DE=![]() AD.
AD.
解:(1)∵正方形![]() 的对角线
的对角线![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
∵![]() ,∴
,∴![]()
∴![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
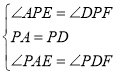
∴![]()
![]()
![]() ,
,
∴![]() ,
,
∴![]() ,
,
(2)方法一:如图②,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵四边形![]() 为菱形,
为菱形,
∴![]() ,
,![]() ,
,![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
又∵![]() ,
,
∴![]()
又∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]()
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
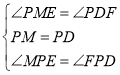
∴![]()
![]()
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
方法二:如图②,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵四边形![]() 为菱形,
为菱形,
∴![]() ,
,![]()
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,
又∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
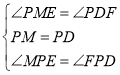
∴![]()
![]()
![]() ,
,
∴![]() ,
,
∴![]() ,
,
(3)
在整个运动变化过程中,
①当点![]() 落在
落在![]() 上时,方法同上可得:
上时,方法同上可得:![]() ,
,
②当点![]() 落在
落在![]() 的延长线上时,取AD中点M,连接PM,
的延长线上时,取AD中点M,连接PM,
如图③,
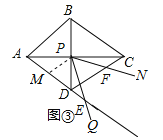
∵四边形ABCD为菱形,∠ADC=120°,
∴AD=CD,∠DAP=30°,AC⊥BD,
∴∠ADP=∠CDP=60°,
∵AM=MD,
∴PM=MD,
∴△MDP是等边三角形,
∴∠PME=∠MPD=60°,PM=PD,
∵∠QPN=60°,
∴∠MPE=∠FPD,
在△MPE和△DPF中,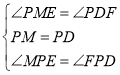
∴△MPE≌△DPF(ASA).
∴ME=DF,
∴DF-DE=![]() AD.
AD.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)如图①,若点D是抛物线上一动点,设点D的横坐标为m(0<m<3),连接CD,BD,BC,AC,当△BCD的面积等于△AOC面积的2倍时,求m的值;
(3)若点N为抛物线对称轴上一点,请在图②中探究抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西省第十五届运动会乒乓球比赛于2018年8月13日上午在山西省体育博物馆的比赛场馆内正式拉开了帷幕.第十五届运动会竞技体育组乒乓球项目产生的决赛运动员名单中太原市共27人,其中甲组有甲、乙、丙、丁四名女子运动员,若进行一次乒乓球单打比赛,要通过抽签从中选出两名运动员打第一场比赛.
(1)若已确定甲打第一场,再从其余三名运动员中随机选取一位,求恰好选中乙的概率;
(2)若两名运动员都不确定,请用树状图法或列表法,求恰好选中甲、乙两名运动员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
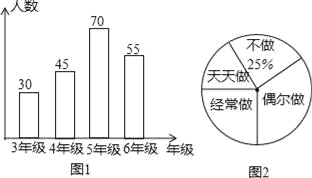
【题目】“热爱劳动,勤俭节约”是中华民族的光荣传统,某小学校为了解本校3至6年级的3000名学生帮助父母做家务的情况,以便做好引导和教育工作,随机抽取了200名学生进行调查,按年级人数和做家务程度,分别绘制了条形统计图(图1)和扇形统计图(图2).
(1)四个年级被调查人数的中位数是多少?
(2)如果把“天天做”、“经常做”、“偶尔做”都统计成帮助父母做家务,那么该校3至6年级学生帮助父母做家务的人数大约是多少?
(3)在这次调查中,六年级共有甲、乙、丙、丁四人“天天帮助父母做家务”,现准备从四人中随机抽取两人进行座谈,请用列表法或画树状图的方法求出抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
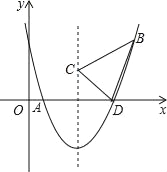
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
(1)求二次函数的解析式;
(2)求函数图象的顶点坐标及D点的坐标;
(3)二次函数的对称轴上是否存在一点C,使得△CBD的周长最小?若C点存在,求出C点的坐标;若C点不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,足球场上守门员在![]() 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的![]() 处飞出(
处飞出(![]() 在
在![]() 轴上),运动员乙在距
轴上),运动员乙在距![]() 点6米的
点6米的![]() 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点![]() ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
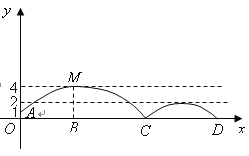
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点![]() 距守门员多少米?(取
距守门员多少米?(取![]() )
)
(3)运动员乙要抢到第二个落点![]() ,他应再向前跑多少米?
,他应再向前跑多少米?
(取![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=![]() ,且经过点(2,0),下列说法:
,且经过点(2,0),下列说法:
①abc<0;
②a+b=0;
③4a+2b+c<0;
④若(﹣2,y1),(﹣3,y2)是抛物线上的两点,则y1<y2,
其中说法正确的是( )
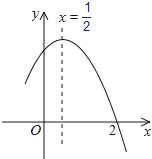
A. ①②④ B. ③④ C. ①③④ D. ①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com