
【题目】定义:如果一个三角形一条边上的高与这条边的比值是3:5,那么称这个三角形为“准黄金”三角形,这条边就叫做这个三角形的“金底”.
(概念感知)
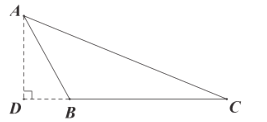
(1)如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,试判断
,试判断![]() 是否是“准黄金”三角形,请说明理由.
是否是“准黄金”三角形,请说明理由.

(问题探究)
(2)如图2,![]() 是“准黄金”三角形,BC是“金底”,把
是“准黄金”三角形,BC是“金底”,把![]() 沿BC翻折得到
沿BC翻折得到![]() ,连AB接AD交BC的延长线于点E,若点C恰好是
,连AB接AD交BC的延长线于点E,若点C恰好是![]() 的重心,求
的重心,求![]() 的值.
的值.
(拓展提升)
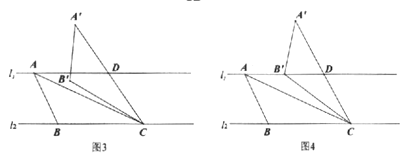
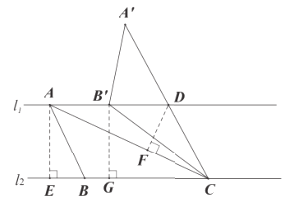
(3)如图3,![]() ,且直线
,且直线![]() 与
与![]() 之间的距离为3,“准黄金”
之间的距离为3,“准黄金”![]() 的“金底”BC在直线
的“金底”BC在直线![]() 上,点A在直线
上,点A在直线![]() 上.
上.![]() ,若
,若![]() 是钝角,将
是钝角,将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,线段
,线段![]() 交
交![]() 于点D.
于点D.
①当![]() 时,则
时,则![]() _________;
_________;
②如图4,当点B落在直线![]() 上时,求
上时,求![]() 的值.
的值.
【答案】(1)![]() 是“准黄金”三角形,理由见解析;(2)
是“准黄金”三角形,理由见解析;(2)![]() ;(3)①
;(3)①![]() ;②
;②![]() .
.
【解析】
(1)过点A作![]() 于点D,先求出AD的长度,然后得到
于点D,先求出AD的长度,然后得到![]() ,即可得到结论;
,即可得到结论;
(2)根据题意,由“金底”的定义得![]() ,设
,设![]() ,
,![]() ,由勾股定理求出AB的长度,根据比值即可求出
,由勾股定理求出AB的长度,根据比值即可求出![]() 的值;
的值;
(3)①作AE⊥BC于E,DF⊥AC于F,先求出AC的长度,由相似三角形的性质,得到AF=2DF,由解直角三角形,得到![]() ,则
,则![]() ,即可求出DF的长度,然后得到CD的长度;
,即可求出DF的长度,然后得到CD的长度;
②由①可知,得到CE和AC的长度,分别过点![]() ,D作
,D作![]() ,
,![]() ,垂足分别为点G,F,然后根据相似三角形的判定和性质,得到
,垂足分别为点G,F,然后根据相似三角形的判定和性质,得到![]() ,然后求出CD和AD的长度,即可得到答案.
,然后求出CD和AD的长度,即可得到答案.
解:(1)![]() 是“准黄金”三角形.
是“准黄金”三角形.
理由:如图,过点A作![]() 于点D,
于点D,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() 是“准黄金”三角形.
是“准黄金”三角形.
(2)∵点A,D关于BC对称,
∴![]() ,
,![]() .
.
∵![]() 是“准黄金”三角形,BC是“金底”,
是“准黄金”三角形,BC是“金底”,
∴![]() .
.
不防设![]() ,
,![]() ,
,
∵点![]() 为
为![]() 的重心,
的重心,
∴![]() .
.
∴![]() ,
,![]() .
.
∴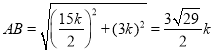 .
.
∴![]() .
.
(3)①作AE⊥BC于E,DF⊥AC于F,如图:
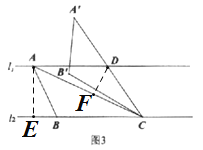
由题意得AE=3,
∵![]() ,
,
∴BC=5,
∵![]() ,
,
∴![]() ,
,
在Rt△ABE中,由勾股定理得:
![]() ,
,
∴![]() ,
,
∴![]() ;
;
∵∠AEC=∠DFA=90°,∠ACE=∠DAF,
∴△ACE∽△DAF,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∵∠ACD=30°,
∴![]() ,
,
∴![]() ,
,
解得:![]()
∴![]() .
.
②如图,过点A作![]() 于点E,则
于点E,则![]() .
.
∵![]() 是“准黄金”三角形,BC是“金底”,
是“准黄金”三角形,BC是“金底”,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
分别过点![]() ,D作
,D作![]() ,
,![]() ,垂足分别为点G,F,
,垂足分别为点G,F,
∴![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴设![]() ,
,![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,且
,且![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() ,解得
,解得![]() .
.
∴![]() ,
,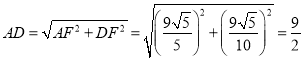 .
.
∴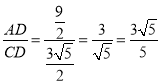 .
.


科目:初中数学 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
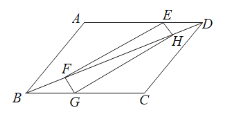
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD ,BC上,顶点F,H在菱形ABCD的对角线BD上,若AB=6,∠A=120°,且DE=2,则FH=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
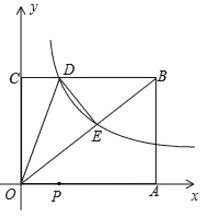
【题目】如图,已知矩形![]() 的两边OA,OC分别落在
的两边OA,OC分别落在![]() 轴,
轴,![]() 轴的正半轴上,
轴的正半轴上,![]() 的坐标为
的坐标为![]() ,反比例函数
,反比例函数![]() 的图象经过
的图象经过![]() 的中点E,且与BC边相交于点D.
的中点E,且与BC边相交于点D.
(1)①求反比例函数的解析式及点D的坐标;
②直接写出![]() 的面积为________.
的面积为________.
(2)若P是OA上的动点,当![]() 值为最小时,求直线
值为最小时,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,顶点为![]() 的抛物线
的抛物线![]() 与
与![]() 轴的另一个交点为
轴的另一个交点为![]() ,连接
,连接![]() .
.
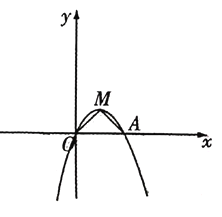
(1)求抛物线![]() 的函数表达式;
的函数表达式;
(2)已知点![]() 的坐标为
的坐标为![]() ,将抛物线
,将抛物线![]() 向上平移得到抛物线
向上平移得到抛物线![]() ,抛物线
,抛物线![]() 与
与![]() 轴分别交于点
轴分别交于点![]() (点
(点![]() 在点
在点![]() 的左侧),如果
的左侧),如果![]() 与
与![]() 相似,求所有符合条件的抛物线
相似,求所有符合条件的抛物线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
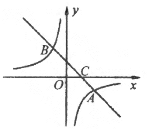
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于
的图像交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)请直接写出不等式![]() 的解集;
的解集;
(3)将![]() 轴下方的图像沿
轴下方的图像沿![]() 轴翻折,点
轴翻折,点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
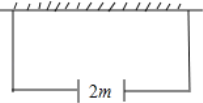
【题目】如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m.围成长方形的养鸡场除门之外四周不能有空隙.
(1)若墙长为18m,要围成养鸡场的面积为150m2,则养鸡场的长和宽各为多少?
(2)围成养鸡场的面积能否达到200m2?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备开办“书画、器乐、戏曲、棋类”四个兴趣班.为了解学生对兴趣班的选择情况,随机抽取部分学生调查.每人单选一项,结果如下(尚未完善).
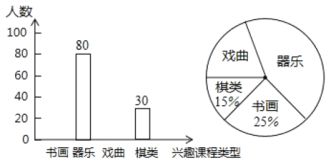
![]() 求本次调查的学生人数和扇形图中“器乐”对应圆心角的大小.
求本次调查的学生人数和扇形图中“器乐”对应圆心角的大小.
![]() 若全校共有
若全校共有![]() 名学生,请估计选择“戏曲”的人数.
名学生,请估计选择“戏曲”的人数.
![]() 学校将从四个兴趣班中任选取两个参加全区青少年才艺展示活动,求恰好抽到“器乐”和“戏曲”的概率.
学校将从四个兴趣班中任选取两个参加全区青少年才艺展示活动,求恰好抽到“器乐”和“戏曲”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com