
【题目】如图所示,抛物线y=![]() ﹣
﹣![]() x﹣4与x轴交于点A、B,与y 轴相交于点C.
x﹣4与x轴交于点A、B,与y 轴相交于点C.
(1)求直线BC的解析式;
(2)将直线BC向上平移后经过点A得到直线l:y=mx+n,点D在直线l上,若以A、B、C、D为顶点的四边形是平行四边形,求出点D的坐标.
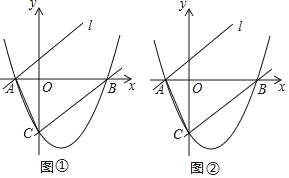
【答案】(1)直线的解析式为y=![]() x﹣4;(2)点D的坐标为(4,4)或(﹣8,﹣4).
x﹣4;(2)点D的坐标为(4,4)或(﹣8,﹣4).
【解析】分析:(1)根据自变量与函数值得对应关系,可得A,B,C的坐标,根据待定系数法,可得答案;
(2)根据平行线的关系,可得m的值,根据待定系数法,可得n的值,根据勾股定理,可得AD,根据平行线的性质,可得关于x的方程,根据解方程,可得x值,再根据自变量与函数值得对应关系,可得D点坐标.
详解:(1)令y=0,得![]() x2-
x2-![]() x-4=0,
x-4=0,
解得:x1=-2,x2=6,
则得点A(-2,0),点B(6,0);
令x=0,得y=-4,
得点C(0,-4).
设直线BC的解析式为y=kx+b,由题意得:
![]() ,
,
解得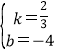 ,
,
∴直线的解析式为y=![]() x-4;
x-4;
(2)由将直线BC向上平移后经过点A得到直线:y=mx+n,
∴m=![]() ,
,
即y=![]() x+n,则
x+n,则![]() ×(-2)+n=0,
×(-2)+n=0,
∴n=![]() ,
,
则直线的解析式为:y=![]() x+
x+![]() ,
,
若以A、B、C、D为顶点的四边形是平行四边形,又AD∥BC,
∴AD=BC.
∵点在直线l上,设点D的坐标为(x,![]() x+
x+![]() ),过点D作DE⊥AB于E,
),过点D作DE⊥AB于E,
则AE2+DE2=AD2,又AD=BC![]() ,
,
∴(x+2)2+(![]() x+
x+![]() )2=52,
)2=52,
解得:x1=4,x2=-8.
当x=4时,![]() x+
x+![]() =4;
=4;
当x=-8时,![]() x+
x+![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A在x轴的正半轴上,顶点D在y轴的正半轴上,点B、点C在第一象限,sin∠OAD=![]() ,线段AD、AB的长分别是方程x2﹣11x+24=0的两根(AD>AB).
,线段AD、AB的长分别是方程x2﹣11x+24=0的两根(AD>AB).
(1)求点B的坐标;
(2)求直线AB的解析式;
(3)在直线AB上是否存在点M,使以点C、点B、点M为顶点的三角形与△OAD相似?若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是![]() 的切线,切点为A,AB是
的切线,切点为A,AB是![]() 的弦,过点B作
的弦,过点B作![]() ,交
,交![]() 于点C,连接AC,过点C作
于点C,连接AC,过点C作![]() ,交AD于点D,连接AO并延长AO交BC于点M,交
,交AD于点D,连接AO并延长AO交BC于点M,交![]() 于点E,交过点C的直线于点P,且
于点E,交过点C的直线于点P,且![]() .
.
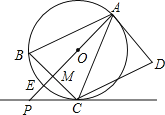
![]() 求证:
求证:![]() ;
;
![]() 判断直线PC与
判断直线PC与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 若
若![]() ,
,![]() ,求PC的长.
,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打![]() 折售票,节假日按团队人数分段定价售票,即
折售票,节假日按团队人数分段定价售票,即![]() 人以下(含
人以下(含![]() 人)的团队按原价售票;超过
人)的团队按原价售票;超过![]() 人的团队,其中
人的团队,其中![]() 人仍按原价售票,超过
人仍按原价售票,超过![]() 人部分的游客打
人部分的游客打![]() 折售票.设某旅游团人数为
折售票.设某旅游团人数为![]() 人,非节假日购票款为
人,非节假日购票款为![]() (元),节假日购票款为
(元),节假日购票款为![]() (元).
(元).![]() 与
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
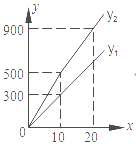
(1)观察图象可知:![]() ;
;![]() ;
;![]() ;
;
(2)直接写出![]() ,
,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)某旅行社导游王娜于5月1日带![]() 团,5月20日(非节假日)带
团,5月20日(非节假日)带![]() 团都到该景区旅游,共付门票款1900元,
团都到该景区旅游,共付门票款1900元,![]() ,
,![]() 两个团队合计50人,求
两个团队合计50人,求![]() ,
,![]() 两个团队各有多少人?
两个团队各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学决定在本校学生中开展足球、篮球、羽毛球、乒乓球四种活动,为了了解学生对这四种活动的喜爱情况,学校随机调查了该校m名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.请你根据图中的信息,解答下列问题.
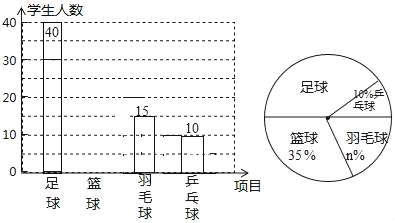
(1)m= ,n= ;
(2)请补全图中的条形图;
(3)扇形统计图中,足球部分的圆心角是 度;
(4)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱踢足球.
查看答案和解析>>
科目:初中数学 来源: 题型:
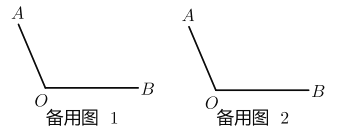
【题目】已知:点![]() 在同一条直线上,点
在同一条直线上,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点.
的中点.
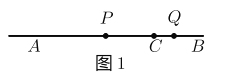
(1)如图1 ,当点![]() 在线段
在线段![]() 上时.
上时.
①若![]() ,则线段
,则线段![]() 的长为_______.
的长为_______.
②若点![]() 为线段
为线段![]() 上任意一点,
上任意一点, ![]() ,则线段
,则线段![]() 的长为_______. ( 用含
的长为_______. ( 用含![]() 的代数式表示)
的代数式表示)
(2)如图2 ,当点![]() 不在线段
不在线段![]() 上时,若
上时,若![]() ,求
,求![]() 的长(用含
的长(用含![]() 的代数式表示) .
的代数式表示) .
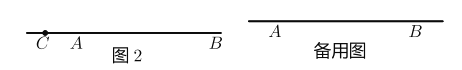
(3)如图,已知![]() ,作射线
,作射线![]() ,若射线
,若射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .
.
①当射线![]() 在
在![]() 的内部时,则
的内部时,则![]() =________°.
=________°.
②当射线![]() 在
在 ![]() 的外部时,则
的外部时,则![]() =_______°. ( 用含
=_______°. ( 用含![]() 的代数式表示) .
的代数式表示) .
查看答案和解析>>
科目:初中数学 来源: 题型:
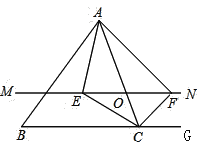
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上的一个动点,过点
边上的一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的角平分线于点
的角平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并证明你的结论.
是矩形?并证明你的结论.
(3)当点![]() 运动到何处,且
运动到何处,且![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?并说明理由.
是正方形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以20米/秒的速度行驶时,A处受噪音影响的时间为( )

A. 16秒B. 18秒C. 20秒D. 22秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com