
【题目】如图,M为正方形ABCD边AB的中点,E是AB延长线上的一点,MN⊥DM,且交∠CBE的平分线于N.
(1)求证:MD=MN;
(2)若将上述条件中的“M为AB边的中点”改为“M为AB边上任意一点”,其余条件不变,则结论“MD=MN”成立吗?如果成立,请证明;如果不成立,说明理由.

【答案】(1)详见解析;(2)成立,理由详见解析.
【解析】
(1)要证MD=MN,就要构建△DFM≌△MBN,只需取AD的中点F,连接FM,依据正方形的性质可证
(2)只需作AF=AM,其余证法与1同.
解:(1)证明:取AD的中点F,连接MF.
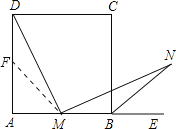
∵四边形ABCD是正方形,M是AB的中点,
∴∠A=∠ABC=90°,DF=AF=AM=MB,
∴∠AFM=45°.
又∵BN平分∠CBE,
∴∠EBN=45°,
∴∠EBN=∠AFM,
∴∠DFM=∠MBN.
又∵∠FDM+∠DMA=90°,
∠BMN+∠DMA=90°,
∴∠FDM=∠BMN,
∴△FDM≌△BMN,∴MD=NM.
(2)结论“MD=NM”仍然成立.
理由:与(1)类似,在AD上截取DF=MB,连接M.
易得∠FDM=∠BMN,∠DFM=∠MBN,
从而△FDM≌△BMN,∴MD=NM.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AF平分∠BAD交BC于E,交DC延长线于F,点G为EF的中点,连结DG.
(1)求证:BC=DF;
(2)连BD,求BD:DG的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人驾车分别从A,B两地同时出发,相向而行.下图是二人离A地的距离y(千米)与所用时间x(小时)的关系.
(1)请说明交点P所表示的实际意义: ;
(2)试求出A,B两地之间的距离;
(3)甲从A地到达B地所需的时间为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明过程,并在括号中填上理论依据.
如图,已知AC⊥AE垂足为A,BD⊥BF垂足为B,∠1=35°,∠2=35°.

证明:AC∥BD; AE∥BF.
证明:∵∠1=∠2=35°,
∴ ∥ ( )
∵AC⊥AE,BD⊥BF,
∴∠ =∠ =90°
又∵∠1=∠2=35°,
∴∠ =∠
∴EA∥BF( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中, BD是∠ABC的平分线,过点C作CE⊥BD,交 BD的延长线于点E,∠ABC=60°,∠ECD=15°.
(1)直接写出∠ADB的度数是_______;
(2)求证:BD=AB;
(3)若AB=2,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人想共同承包一项工程,甲单独做30天完成,乙单独做20天完成,合同规定15天完成,否则每超过1天罚款1 000元,甲、乙两人经商量后签订了该合同.
(1)正常情况下,甲、乙两人能否履行该合同?为什么?
(2)现两人合作了这项工程的75%,因别处有急事,必须调走1人,问调走谁更合适些?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 ![]() 的图像交
的图像交 ![]() 轴于
轴于 ![]() ,交
,交 ![]() 轴于点
轴于点 ![]() ,连接直线
,连接直线 ![]() .
.
(1)求二次函数的解析式;
(2)点 ![]() 在二次函数的图像上,圆
在二次函数的图像上,圆 ![]() 与直线
与直线 ![]() 相切,切点为
相切,切点为 ![]() .
.
①若 ![]() 在
在 ![]() 轴的左侧,且△
轴的左侧,且△ ![]() ∽△
∽△ ![]() ,求点
,求点 ![]() 的坐标;
的坐标;
②若圆 ![]() 的半径为4,求点
的半径为4,求点 ![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com