
【题目】小明和小亮进行100米赛跑,两人在同一起跑线上,结果第一次比赛时小明胜10米;在进行第二次比赛时,小明的起跑线比原来起跑线推后10米,如果两次他们速度不变,则第二次结果( )胜.
A.小亮胜B.小明胜C.同时到达D.不能确定
科目:初中数学 来源: 题型:
【题目】在2018春季环境整治活动中,某社区计划对面积为1600m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用5天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y关于x的函数关系式;
(3)若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过25天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:求若干个相同的有理数(均不等于 0)的除法运算叫做除方,如 2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等,类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈 3 次方,”(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作:“(﹣3)的圈 4 次方”.一般地,把![]() 个记作 a,读作 “a 的圈 n次方”
个记作 a,读作 “a 的圈 n次方”
(初步探究)
(1)直接写出计算结果:2③,(﹣![]() )③.
)③.
(深入思考)
2③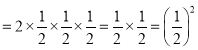
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
(2)试一试,仿照上面的算式,将下列运算结果直接写成幂的形式.5⑥;(﹣![]() )⑩.
)⑩.
(3)猜想:有理数 a(a≠0)的圈n(n≥3)次方写成幂的形式等于多少.
(4)应用:求(-3)8×(-3)⑨-(﹣![]() )9×(﹣
)9×(﹣![]() )⑧
)⑧
查看答案和解析>>
科目:初中数学 来源: 题型:
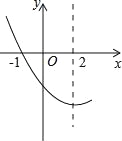
【题目】如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(﹣1,0).有下列结论:
①abc>0;②4a﹣2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤点(﹣3,y1),(6,y2)都在抛物线上,则有y1<y2.
其中正确的是( )
A.①②③ B.②④⑤ C.①③④ D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com