
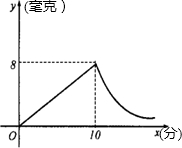
 例(这两个变量之间的关系如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8毫克.据以上信息解答下列问题:
例(这两个变量之间的关系如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8毫克.据以上信息解答下列问题: .
. x.
x.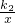 (k2≠0),
(k2≠0),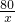 .
.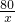 =
=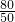 =1.6.
=1.6.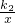 (k2≠0),然后由(10,8)在函数图象上,利用待定系数法即可求得药物燃烧阶段后y与x的函数解析式;
(k2≠0),然后由(10,8)在函数图象上,利用待定系数法即可求得药物燃烧阶段后y与x的函数解析式;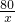 ,即可求得y的值,则可求得答案.
,即可求得y的值,则可求得答案.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
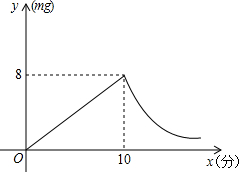 烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8 mg.根据以上信息,解答下列问题:
烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8 mg.根据以上信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
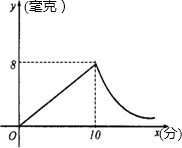 例(这两个变量之间的关系如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8毫克.据以上信息解答下列问题:
例(这两个变量之间的关系如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8毫克.据以上信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•淮北模拟)某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题:
(2012•淮北模拟)某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题:
示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 含药量为8mg.据以上信息解答下列问题:
含药量为8mg.据以上信息解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com