
分析 (1)根据有理数的加法和减法可以解答本题;
(2)根据有理数的乘除法和减法可以解答本题.
解答 解:(1)(-28$\frac{1}{3}$)-(-22)-(-17$\frac{1}{3}$)+(-22)
=(-28$\frac{1}{3}$)+22+17$\frac{1}{3}$+(-22)
=[(-28$\frac{1}{3}$)+17$\frac{1}{3}$]+[22+(-22)]
=-11;
(2)(-100)÷(-5)2-(-$\frac{1}{5}$)×[34+(-32)]
=(-100)×$\frac{1}{25}$-(-$\frac{1}{5}$)×[34-9]
=(-4)+$\frac{1}{5}$×25
=(-4)+5
=1.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法,注意能用简便方法的用简便方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF.求证:
如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线y=$\frac{1}{3}$x+1与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
如图,已知直线y=$\frac{1}{3}$x+1与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
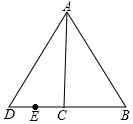 如图,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD.
如图,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
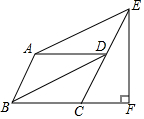 如图,在?ABCD中,∠BCD=120°,连接BD,过点A作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,若CF=2,则AB=2.
如图,在?ABCD中,∠BCD=120°,连接BD,过点A作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,若CF=2,则AB=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com