
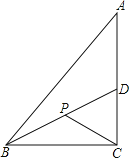
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,点
,点![]() 是
是![]() 的中点,若
的中点,若![]() ,则
,则![]() 的长为__________.
的长为__________.
【答案】3
【解析】
过点D作DE⊥AB于E,根据直角三角形两锐角互余求出∠A=30°,再根据直角三角形30°角所对的直角边等于斜边的一半求出DE,根据角平分线上的点到角的两边距离相等可得CD=DE,根据角平分线的定义求出∠CBD=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出BD,再根据直角三角形斜边上的中线等于斜边的一半求解.
如图,过点D作DE⊥AB于E,
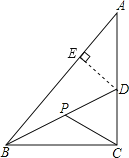
∵∠ACB=90°,∠ABC=60°,
∴∠A=90°-60°=30°,
∴DE=![]() AD=
AD=![]() ×6=3,
×6=3,
又∵BD平分∠ABC,
∴CD=DE=3,
∵∠ABC=60°,BD平分∠ABC,
∴∠CBD=30°,
∴BD=2CD=2×3=6,
∵P点是BD的中点,
∴CP=![]() BD=
BD=![]() ×6=3.
×6=3.
故答案为:3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上一个动点,连结
上一个动点,连结![]() ,过
,过![]() 作
作![]() ,
,![]() ,
,
![]() ,
,![]() 分别为垂足.
分别为垂足.
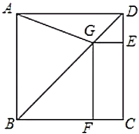
(1)求证:![]() ;
;
(2)①写出![]() 、
、![]() 、
、![]() 三条线段满足的等量关系,并证明;②求当
三条线段满足的等量关系,并证明;②求当![]() ,
,![]() 时,
时,![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
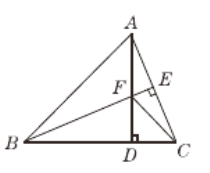
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证△ACD≌△BFD
(2)求证:BF=2AE;
(3)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
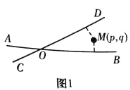
【题目】定义:如图1,平面上两条直线AB、CD相交于点O,对于平面内任意一点M,点M到直线AB、CD的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”为(0,0)的点有1个,即点O.
(1)“距离坐标”为1,0的点有 个;
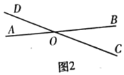
(2)如图2,若点M在过点O且与直线AB垂直的直线l上时,点M的“距离坐标”为p,q,且BOD 150,请写出p、q的关系式并证明;
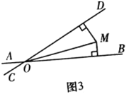
(3)如图3,点M的“距离坐标”为![]() ,且DOB 30,求OM的长.
,且DOB 30,求OM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
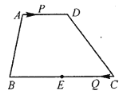
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点.点
的中点.点![]() 以每秒1个单位长度的速度从点
以每秒1个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动;同时,点
运动;同时,点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动.点
运动.点![]() 停止运动时,点
停止运动时,点![]() 也随之停止运动.求当运动时间
也随之停止运动.求当运动时间![]() 为多少秒时,以点
为多少秒时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
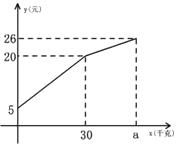
【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
查看答案和解析>>
科目:初中数学 来源: 题型:
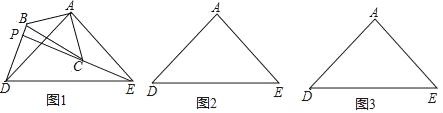
【题目】如图所示,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,EC的延长线交BD于点P.
(1)把△ABC绕点A旋转到图1,BD,CE的关系是 (选填“相等”或“不相等”);简要说明理由;
(2)若AB=3,AD=5,把△ABC绕点A旋转,当∠EAC=90°时,在图2中作出旋转后的图形,PD= ,简要说明计算过程;
(3)在(2)的条件下写出旋转过程中线段PD的最小值为 ,最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
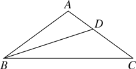
【题目】如图,在△ABC中,AB=AC,∠A=108°,BD平分∠ABC交AC于点D.
(1)填空:∠DBC=_________度;
(2)猜想:BC、AB、CD三者数量关系_____________________;
(3)证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,两条垂线相交于点
,两条垂线相交于点![]() .
.
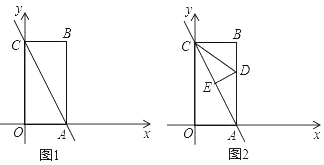
(1)线段![]() ,
,![]() ,
,![]() 的长分别为
的长分别为![]() _______,
_______,![]() _________,
_________,![]() _________;
_________;
(2)折叠图1中的![]() ,使点
,使点![]() 与点
与点![]() 重合,再将折叠后的图形展开,折痕
重合,再将折叠后的图形展开,折痕![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,如图2.
,如图2.
①求线段![]() 的长;
的长;
②在![]() 轴上,是否存在点
轴上,是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,请直接写出符合条件的所有点
为等腰三角形?若存在,请直接写出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com