
【题目】如图1,二次函数y=﹣x2+bx+c的图象过点A(3,0),B(0,4)两点,动点P从A出发,在线段AB上沿A→B的方向以每秒2个单位长度的速度运动,过点P作PD⊥y于点D,交抛物线于点C.设运动时间为t(秒).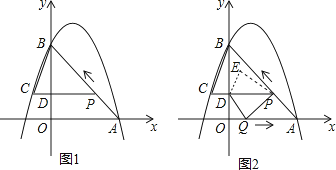
(1)求二次函数y=﹣x2+bx+c的表达式;
(2)连接BC,当t= ![]() 时,求△BCP的面积;
时,求△BCP的面积;
(3)如图2,动点P从A出发时,动点Q同时从O出发,在线段OA上沿O→A的方向以1个单位长度的速度运动.当点P与B重合时,P、Q两点同时停止运动,连接DQ,PQ,将△DPQ沿直线PC折叠得到△DPE.在运动过程中,设△DPE和△OAB重合部分的面积为S,直接写出S与t的函数关系及t的取值范围.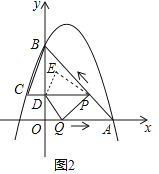
【答案】
(1)
解:把A(3,0),B(0,4)代入y=﹣x2+bx+c中得:
![]() 解得
解得 ![]() ,
,
∴二次函数y=﹣x2+bx+c的表达式为:y=﹣x2+ ![]() x+4
x+4
(2)
解:如图1,
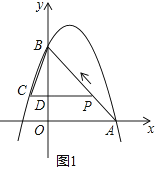
当t= ![]() 时,AP=2t,
时,AP=2t,
∵PC∥x轴,
∴ ![]() ,
,
∴ ![]() ,
,
∴OD= ![]() =
= ![]() ×
× ![]() =
= ![]() ,
,
当y= ![]() 时,
时, ![]() =﹣x2+
=﹣x2+ ![]() x+4,
x+4,
3x2﹣5x﹣8=0,
x1=﹣1,x2= ![]() ,
,
∴C(﹣1, ![]() ),
),
由 ![]() 得
得 ![]() ,
,
则PD=2,
∴S△BCP= ![]() ×PC×BD=
×PC×BD= ![]() ×3×
×3× ![]() =4
=4
(3)
解:如图3,

当点E在AB上时,
由(2)得OD=QM=ME= ![]() ,
,
∴EQ= ![]() ,
,
由折叠得:EQ⊥PD,则EQ∥y轴
∴ ![]() ,
,
∴ ![]() ,
,
∴t= ![]() ,
,
同理得:PD=3﹣ ![]() ,
,
∴当0≤t≤ ![]() 时,S=S△PDQ=
时,S=S△PDQ= ![]() ×PD×MQ=
×PD×MQ= ![]() ×(3﹣
×(3﹣ ![]() )×
)× ![]() ,
,
S=﹣ ![]() t2+
t2+ ![]() t;
t;
当 ![]() <t≤2.5时,
<t≤2.5时,
如图4,
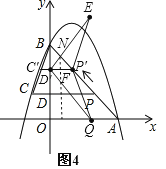
P′D′=3﹣ ![]() ,
,
点Q与点E关于直线P′C′对称,则Q(t,0)、E(t, ![]() ),
),
∵AB的解析式为:y=﹣ ![]() x+4,
x+4,
D′E的解析式为:y= ![]() x+
x+ ![]() t,
t,
则交点N( ![]() ,
, ![]() ),
),
∴S=S△P′D′N= ![]() ×P′D′×FN=
×P′D′×FN= ![]() ×(3﹣
×(3﹣ ![]() )(
)( ![]() ﹣
﹣ ![]() ),
),
∴S= ![]() t2﹣
t2﹣ ![]() t+
t+ ![]() .
.
【解析】(1)直接将A、B两点的坐标代入列方程组解出即可;(2)如图1,要想求△BCP的面积,必须求对应的底和高,即PC和BD;先求OD,再求BD,PC是利用点P和点C的横坐标求出,要注意符号;(3)分两种情况讨论:①△DPE完全在△OAB中时,即当0≤t≤ ![]() 时,如图2所示,重合部分的面积为S就是△DPE的面积;②△DPE有一部分在△OAB中时,当
时,如图2所示,重合部分的面积为S就是△DPE的面积;②△DPE有一部分在△OAB中时,当 ![]() <t≤2.5时,如图4所示,△PDN就是重合部分的面积S.本题是二次函数的综合题,考查了利用待定系数法求二次函数和一次函数的解析式,并能利用方程组求出两图象的交点,把方程和函数有机地结合在一起,使函数问题简单化;同时考查了分类讨论的思想,这一思想在二次函数中经常运用,要熟练掌握;本题还与相似结合,利用相似三角形对应边的比来表示线段的长.
<t≤2.5时,如图4所示,△PDN就是重合部分的面积S.本题是二次函数的综合题,考查了利用待定系数法求二次函数和一次函数的解析式,并能利用方程组求出两图象的交点,把方程和函数有机地结合在一起,使函数问题简单化;同时考查了分类讨论的思想,这一思想在二次函数中经常运用,要熟练掌握;本题还与相似结合,利用相似三角形对应边的比来表示线段的长.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图.

(1)填写下列各点的坐标:A4( , ),A8( , );
(2)点A4n﹣1的坐标(n是正整数)为
(3)指出蚂蚁从点A2013到点A2014的移动方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.

(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.
(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?(不需说明理由)
②是否存在满足条件的点P,使得PC= ![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( ) 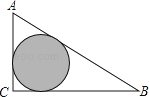
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实省新课改精神,我是各校都开设了“知识拓展类”、“体艺特长类”、“实践活动类”三类拓展性课程,某校为了解在周二第六节开设的“体艺特长类”中各门课程学生的参与情况,随机调查了部分学生作为样本进行统计,绘制了如图所示的统计图(部分信息未给出)
根据图中信息,解答下列问题:
(1)求被调查学生的总人数;
(2)若该校有200名学生参加了“体艺特长类”中的各门课程,请估计参加棋类的学生人数;
(3)根据调查结果,请你给学校提一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)如图①,在△ABC中,∠ABC的平分线与∠ACB的平分线相交于点P.
(1)若∠ABC=50°,∠ACB=80°,则∠A= 度,∠P= 度
(2)∠A与∠P的数量关系为 ,并说明理由.
(应用)如图②,在△ABC中,∠ABC的平分线与∠ACB的平分线相交于点P.∠ABC的外角平分线与∠ACB的外角平分线相交于点Q.直接写出∠A与∠Q的数量关系为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com