如果两个三角形的三组对应边对应边的比相等.那么这两个三角形相似．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

如果两个三角形的三组

对应边

的比相等，那么这两个三角形相似．

分析：根据三边法：三组对应边的比相等的两个三角形相似作答

解答：解：如果两个三角形的三组对应边的比相等，那么这两个三角形相似．
故答案为：对应边．

点评：考查相似三角形的判定定理：
（1）两角对应相等的两个三角形相似．
（2）两边对应成比例且夹角相等的两个三角形相似．
（3）三边对应成比例的两个三角形相似．

练习册系列答案

同步练习册外语教学与研究出版社系列答案

学习与评价广州出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：阅读理解

阅读材料并解答问题：
我国是最早了解和应用勾股定理的国家之一，古代印度、希腊、阿拉伯等许多国家也都很重视对勾股定理的研究和应用，古希腊数学家毕达哥拉斯首先证明了勾股定理，在西方，勾股定理又称为“毕达哥拉斯定理”．
关于勾股定理的研究还有一个很重要的内容是勾股数组，在《几何》课本中我们已经了解到，“能够成为直角三角形三条边的三个正整数称为勾股数”，以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法：
方法1：若m为奇数（m≥3），则a=m，b=

（m²-1）和c=

（m²+1）是勾股数．
方法2：若任取两个正整数m和n（m＞n），则a=m²-n²，b=2mn，c=m²+n²是勾股数．
（1）在以上两种方法中任选一种，证明以a，b，c为边长的△ABC是直角三角形；
（2）请根据方法1和方法2按规律填写下列表格：

（3）某园林管理处要在一块绿地上植树，使之构成如下图所示的图案景观，该图案由四个全等的直角三角形组成，要求每个三角形顶点处都植一棵树，各边上相邻两棵树之间的距离均为1米，如果每个三角形最短边上都植6棵树，且每个三角形的各边长之比为5：12：13，那么这四个直角三角形的边长共需植树

棵．

查看答案和解析>>

科目：初中数学 来源：学习周报　数学　沪科八年级版　2009－2010学年　第14期　总170期沪科版 题型：013

下列说法：①如果两个三角形可以依据AAS来判定全等，那么一定也可以依据ASA来判定它们全等；②如果两个三角形都和第三个三角形不全等，那么这两个三角形也一定不全等；③要判定两个三角形全等，给出的条件中至少要有一组边对应相等．其中正确的是

[　　]

A．①和②

B．②和③

C．①和③

D．①②③

查看答案和解析>>

科目：初中数学 来源：2014沪科版八年级上册(专题训练　状元笔记)数学：第14章　全等三角形沪科版 题型：044

能够互相重合的多边形叫做全等形，即如果两个多边形对应角相等，对应边相等，那么两个多边形一定全等．但判定两个三角形全等只需三组对应量相等即可，如SAS，SSS等，但如果要判定两个四边形全等仅有四组量对应相等是不够的，必须具备至少五组量对应相等．

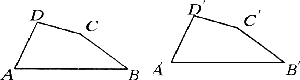
(1)请写出两个四边形全等的一种判定方法(五组量对应相等)；

(2)如图，简要说明你的判定方法是正确的；

(3)举例说明仅有四边对应相等的两个四边形不一定全等(画出图形并简要说明理由)．

查看答案和解析>>

科目：初中数学 来源：初中数学　三点一测丛书　八年级数学　下　（江苏版课标本）江苏版 题型：047

位似三角形

如果两个三角形不仅是相似三角形，而且每组对应点所在的直线都经过同一个点，那么这两个三角形叫做位似三角形，它们的相似比又称为位似比，这个点叫做位

似中心．利用三角形的位似可以将一个三形缩小或放大．

(1)

如图，点O是等边三角形PQR的中心，、、分别是OP、OQ、OR的中点，则△与△PQR是位似三角形．此时，△与△PQR的位似比、位似中心分别为
[　　]
A．	2；点P
B．	；点P
C．	2；点O
D．	；点O