
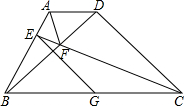
 如图,以线段BC为一边在BC的同侧作Rt△BCD、Rt△BCE,过D作线段DA∥BC,交BE延长线于A,设BD、CE交于点F,取BC的中点G,连接EG、AF,且∠DCB=45°,CD=2.
如图,以线段BC为一边在BC的同侧作Rt△BCD、Rt△BCE,过D作线段DA∥BC,交BE延长线于A,设BD、CE交于点F,取BC的中点G,连接EG、AF,且∠DCB=45°,CD=2.| 2 |
| BD2+CD2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
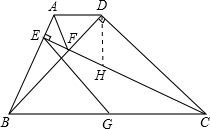 ∵BD⊥CD,BE⊥CE,
∵BD⊥CD,BE⊥CE,

科目:初中数学 来源: 题型:
 (2013•平谷区一模)如图,在直角坐标系中,已知直线y=
(2013•平谷区一模)如图,在直角坐标系中,已知直线y=| 1 |
| 2 |
| 5 |
查看答案和解析>>
科目:初中数学 来源:学习周报 数学 北师大八年级版 2009-2010学年 第7期 总第163期 北师大版 题型:044
如图①,在正方形
ABCD中,E是AD的中点,F是BA延长线上的一点,AF=
(1)试说明:△ABE≌△ADF.
(2)阅读下列材料:如图②,把△ABC沿直线平移线段BC的长度,可以变到△ECD的位置;如图③,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;如图④,以点A为中心,把△ABC旋转180°,可以变到△AED的位置,像这样其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.

请回答下列问题:
(1)在图①中,可以通过平移、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置?
(2)指出图①中线段BE与DF之间的关系.
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
(1)求证:△ABE≌△ADF.
(2)阅读下列材料:如图②,把△ABC沿直线平移线段BC的长度,可以变到△ECD的位置;如图③,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;如图④,以点A为中心,把△ABC旋转180°,可以变到△AED的位置,像这样其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.

图① 图② 图③ 图④
请回答下列问题:
(1)在图①中,可以通过平移、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置?
(2)指出图①中线段BE与DF之间的关系.
查看答案和解析>>
科目:初中数学 来源:2012年北师大版初中数学八年级上3.5它们是怎样变过来的练习卷(解析版) 题型:解答题
如图①,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF= AB,
AB,
(1)求证:△ABE≌△ADF.
(2)阅读下列材料:如图②,把△ABC沿直线平移线段BC的长度,可以变到△ECD的位置;如图③,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;如图④,以点A为中心,把△ABC旋转180°,可以变到△AED的位置,像这样其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.

图① 图② 图③ 图④
请回答下列问题:
(1)在图①中,可以通过平移、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置?
(2)指出图①中线段BE与DF之间的关系.
查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题
 。
。 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com