
如图,在 中,
中, ,
, ,
, ,
,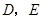 分别是边
分别是边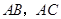 的中点,点
的中点,点 从点
从点 出发沿
出发沿 方向运动,过点
方向运动,过点 作
作 于
于 ,过点
,过点 作
作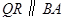 交
交 于
于 ,当点
,当点 与点
与点 重合时,点
重合时,点 停止运动.设
停止运动.设 ,
, .
.

(1)求点 到
到 的距离
的距离 的长;
的长;
(2)求 关于
关于 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点 ,使
,使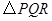 为等腰三角形?若存在,请求出所有满足要求的
为等腰三角形?若存在,请求出所有满足要求的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
解:(1)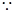
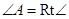 ,
, ,
,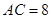 ,
, .
.
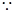 点
点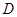 为
为 中点,
中点,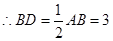 .
.
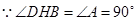 ,
, .
.
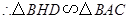 ,
,
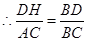 ,
,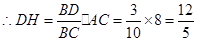 .
.
(2) ,
,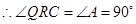 .
.
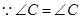 ,
,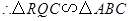 ,
,
 ,
,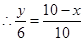 ,
,
即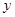 关于
关于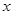 的函数关系式为:
的函数关系式为: .
.
(3)存在,分三种情况:
①当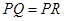 时,过点
时,过点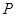 作
作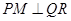 于
于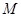 ,则
,则 .
.
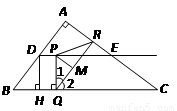
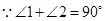 ,
,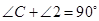 ,
,
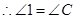 .
.
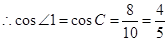 ,
,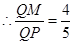 ,
,
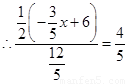 ,
, .
.
②当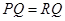 时,
时, ,
,

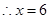 .
.
③当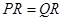 时,则
时,则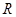 为
为 中垂线上的点,
中垂线上的点,

于是点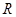 为
为 的中点,
的中点,
 .
.
 ,
,
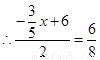 ,
,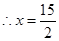 .
.
综上所述,当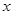 为
为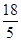 或6或
或6或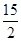 时,
时, 为等腰三角形.
为等腰三角形.
【解析】(1)找出三角形相似的条件(两组角对应相等),根据相似三角形对应边成比例求出 的长;
的长;
(2)利用相似三角形对应边成比例得到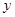 关于
关于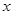 的函数关系式;
的函数关系式;
(3)需分情况讨论哪条边是底还是腰,①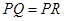 利用同角的余角相等及等角的余弦值相等,得到
利用同角的余角相等及等角的余弦值相等,得到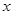 的方程即可;②
的方程即可;②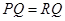 则
则 ;③
;③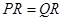 根据到线段的两端点的距离相等的点在线段的垂直平分线上得
根据到线段的两端点的距离相等的点在线段的垂直平分线上得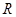 为
为 中垂线上的点,知点
中垂线上的点,知点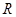 为
为 的中点,根据
的中点,根据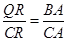 得到
得到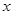 的方程即可。
的方程即可。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2008年初中毕业升学考试(浙江温州卷)数学(带解析) 题型:解答题
如图,在 中,
中, ,
, ,
, ,
, 分别是边
分别是边 的中点,点
的中点,点 从点
从点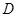 出发沿
出发沿 方向运动,过点
方向运动,过点 作
作 于
于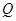 ,过点
,过点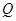 作
作 交
交 于
于 ,当点
,当点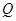 与点
与点 重合时,点
重合时,点 停止运动.设
停止运动.设 ,
, .
.
(1)求点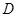 到
到 的距离
的距离 的长;
的长;
(2)求 关于
关于 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点 ,使
,使 为等腰三角形?若存在,请求出所有满足要求的
为等腰三角形?若存在,请求出所有满足要求的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com