

分析 (1)先确定出OA,OB,再由旋转的性质得出OD=4,CD=2,即可得出结论;
(2)先构造出满足条件的点M的位置,利用等腰三角形的性质和等腰直角三角形的性质即可得出结论;
(3)同(2)①的方法得出结论.
解答 解:
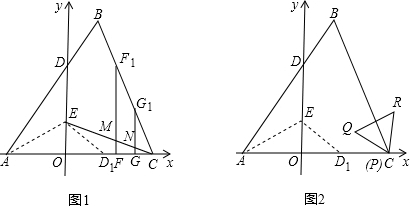
(1)如图1,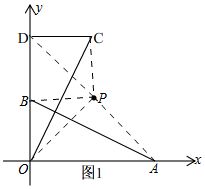
∵点A和点B的坐标分别为A(4,0)、B(0,2),
∴OA=4,OB=2,
由旋转知,△POD≌△PAO,△PCD≌△PBO,
∴OD=OA=4,CD=OB=2,
∴C(2,4),D(0,4);
(2)①如图2,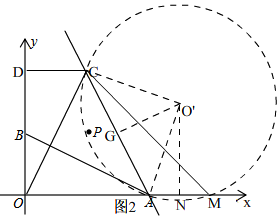
∵A(4,0),C(2,4),
∴AC=2$\sqrt{5}$,
以AC为斜边在直线AC右侧作等腰直角三角形ACO',以O'为圆心,O'A为半径作圆,
∴∠AMC=$\frac{1}{2}$∠AO'C=45°,
过点O'作O'G⊥AC,
∵A(4,0),C(2,4),
∴G(3,2),
∴直线AC的解析式为y=-2x+8,
∴直线O'G的解析式为y=$\frac{1}{2}$x+$\frac{3}{2}$,
设点O'的坐标为(m,$\frac{1}{2}$m+$\frac{1}{2}$),
∴O'G2=(m-3)2+($\frac{1}{2}$m+$\frac{1}{2}$-2)2=($\frac{1}{2}$×$2\sqrt{5}$)2,
∴m=5或m=1(点O'在直线AC右侧,所以舍去),
∴O'(5,3),
∴O'A=$\sqrt{10}$,
在Rt△AO'N中,O'N=3,AN=$\sqrt{O'{A}^{2}-O'{N}^{2}}$=1,
∴AM=2AN=2,
∴M(6,0);
故答案为(6,0),
②如图3,
当∠CAM为直角时,
分别过点C,M作x轴的垂线,垂足分别为E,F.
∵CO=CA,
∴OE=AE=$\frac{1}{2}$OA=2
∴∠CAE+∠ACE=90°,
∵∠CAE+∠FAM=90°,
∴∠ACE=∠FAM,
在△ACE和△MAF中,$\left\{\begin{array}{l}{∠AEC=∠MFA}\\{∠ACE=∠MAF}\\{AC=AM}\end{array}\right.$
∴△CEA≌△AFM,
∴MF=AE=2,AF=CE=4.
∴OF=8,
∴M(8,2);
当∠ACM为直角时,
同理可得M(6,6);
综上所述,点M的坐标为(8,2)或(6,6).
(3)如图3,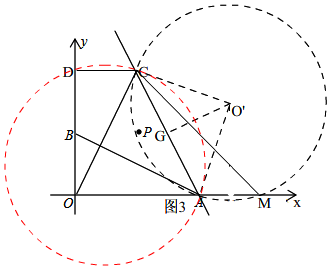
∵A(4,0),C(2,4),
∴AC=2$\sqrt{5}$,
以AC为斜边在直线AC右侧作等腰直角三角形ACO',以O'为圆心,O'A为半径作圆,
∴∠ANC<$\frac{1}{2}$∠AO'C=45°,
过点O'作O'G⊥AC,
∵A(4,0),C(2,4),
∴G(3,2),直线AC的解析式为y=-2x+8,
∴直线O'G的解析式为y=$\frac{1}{2}$x+$\frac{3}{2}$,
设点O'的坐标为(m,$\frac{1}{2}$m+$\frac{1}{2}$),
∴O'G2=(m-3)2+($\frac{1}{2}$m+$\frac{1}{2}$-2)2=($\frac{1}{2}$×$2\sqrt{5}$)2,
∴m=5或m=1,
∴O'(5,3)或(1,1),
∵A(4,0),
∴O'A=$\sqrt{10}$,
∴点N在以点(5,3)或点(1,1)为圆心,以$\sqrt{10}$为半径的圆内.
点评 此题是三角形综合题,主要考查了旋转的性质,等腰直角三角形的和等腰三角形的性质,全等三角形的判定和性质,直角三角形的性质,圆周角定理,解本题的关键是构造出满足条件的图形,是一道比较好的中考常考题.


科目:初中数学 来源: 题型:选择题
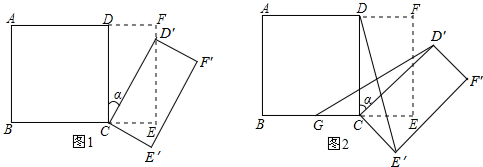
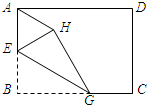 如图,已知长方形纸片ABCD,点E是AB的中点,点G是BC上一点,∠BEG=60°.沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为( )
如图,已知长方形纸片ABCD,点E是AB的中点,点G是BC上一点,∠BEG=60°.沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
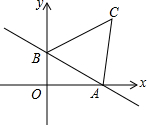 一次函数y=-$\frac{{\sqrt{3}}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内做等边△ABC
一次函数y=-$\frac{{\sqrt{3}}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内做等边△ABC查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
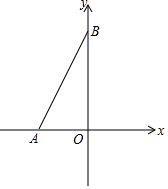 在平面直角坐标系中,A(a,0),B(0,b),且a、b是二元一次方程组$\left\{\begin{array}{l}{a+b-4=0}\\{\frac{1}{2}a-2b+13=0}\end{array}\right.$的解.
在平面直角坐标系中,A(a,0),B(0,b),且a、b是二元一次方程组$\left\{\begin{array}{l}{a+b-4=0}\\{\frac{1}{2}a-2b+13=0}\end{array}\right.$的解.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com