Question

如图，△ABC中，∠ACB=90°，AC=BC，将△ABC绕点C逆时针旋转角α．（0°＜α＜90°）得到△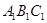，连接．设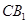交AB于D，分别交AB、AC于E、F．
（1）在图中不再添加其它任何线段的情况下，请你找出一对全等的三角形，并加以说明（△ABC与△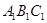全等除外）；
（2）当△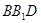是等腰三角形时，求α；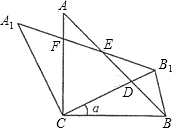

Answer 1

解：（1）全等的三角形有：△CBD≌△CA₁F或△AEF≌△B₁ED或△ACD≌△B₁CF等；
以说明△CBD≌△CA₁F为例：
理由：∵∠ACB₁+∠A₁CF=∠ACB₁+∠BCD=90°
∴∠A₁CF=∠BCD  ∵A₁C=BC   ∴∠A₁=∠CBD=45°  ∴△CBD≌△CA₁F；
（2）在△CBB₁中   ∵CB=CB₁    ∴∠CBB₁=∠CB₁B=1/2（180°-α）
又△ABC是等腰直角三角形  ∴∠ABC=45°
①若B₁B=B₁D，则∠B₁DB=∠B₁BD
∵∠B₁DB=45°+α
∠B₁BD=∠CBB₁-45°=1/2（180°-α）-45°=45°-1/2α    
∴45°+α=45°-α
∴α=0°（舍去）；
②∵∠BB₁C=∠B₁BC＞∠B₁BD，∴BD＞B₁D，即BD≠B₁D；
③若BB₁=BD，则∠BDB₁=∠BB₁D，即45°+α=1/2（180°-α），α=30°
由①②③可知，当△BB₁D为等腰三角形时，α=30°；

解析