
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.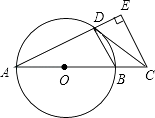
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
【答案】
(1)
证明:连接OD,
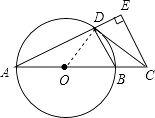
∵CD是⊙O切线,
∴∠ODC=90°,
即∠ODB+∠BDC=90°,
∵AB为⊙O的直径,
∴∠ADB=90°,
即∠ODB+∠ADO=90°,
∴∠BDC=∠ADO,
∵OA=OD,
∴∠ADO=∠A,
∴∠BDC=∠A;
(2)
解:∵CE⊥AE,
∴∠E=∠ADB=90°,
∴DB∥EC,
∴∠DCE=∠BDC,
∵∠BDC=∠A,
∴∠A=∠DCE,
∵∠E=∠E,
∴△AEC∽△CED,
∴ ![]() ,
,
∴EC2=DEAE,
∴16=2(2+AD),
∴AD=6.
【解析】本题考查了切线的性质,相似三角形的判定和性质,平行线的性质,熟练掌握切线的性质是解题的关键.(1)连接OD,由CD是⊙O切线,得到∠ODC=90°,根据AB为⊙O的直径,得到∠ADB=90°,等量代换得到∠BDC=∠ADO,根据等腰直角三角形的性质得到∠ADO=∠A,即可得到结论;(2)根据垂直的定义得到∠E=∠ADB=90°,根据平行线的性质得到∠DCE=∠BDC,根据相似三角形的性质得到 ![]() ,解方程即可得到结论.
,解方程即可得到结论.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】定义:若点P(a,b)在函数y= ![]() 的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=
的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y= ![]() 的一个“派生函数”.例如:点(2,
的一个“派生函数”.例如:点(2, ![]() )在函数y=
)在函数y= ![]() 的图象上,则函数y=2x2+
的图象上,则函数y=2x2+ ![]() x称为函数y=
x称为函数y= ![]() 的一个“派生函数”.现给出以下两个命题:(1)存在函数y=
的一个“派生函数”.现给出以下两个命题:(1)存在函数y= ![]() 的一个“派生函数”,其图象的对称轴在y轴的右侧;(2)函数y=
的一个“派生函数”,其图象的对称轴在y轴的右侧;(2)函数y= ![]() 的所有“派生函数”,的图象都进过同一点.
的所有“派生函数”,的图象都进过同一点.
下列判断正确的是( )
A.命题(1)与命题(2)都是真命题
B.命题(1)与命题(2)都是假命题
C.命题(1)是假命题,命题(2)是真命题
D.命题(1)是真命题,命题(2)是假命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+m的图象与反比例函数y= ![]() 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).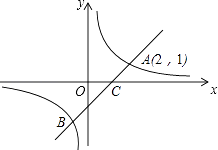
(1)求m及k的值;
(2)求点C的坐标,并结合图象写出不等式组0<x+m≤ ![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF;
(3)若AE=1,EB=2,求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长均相等.网格中三个多边形(分别标记为①,②,③)的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是( )
A.只有②
B.只有③
C.②③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.
(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y= ![]() 的图象相交于A(﹣2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+
的图象相交于A(﹣2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+ ![]() n=0;③S△AOP=S△BOQ;④不等式k1x+b
n=0;③S△AOP=S△BOQ;④不等式k1x+b ![]() 的解集是x<﹣2或0<x<1,其中正确的结论的序号是 .
的解集是x<﹣2或0<x<1,其中正确的结论的序号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将圆形纸片沿弦AB折叠后,圆弧恰好能经过圆心O,⊙O的切线BC与AO延长线交于点C.
(1)若⊙O半径为6cm,用扇形OAB围成一个圆锥的侧面,求这个圆锥的底面圆半径.
(2)求证:AB=BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com