
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的动点,且
上的动点,且![]() ,点
,点![]() 关于
关于![]() 的对称点
的对称点![]() 恰好落在
恰好落在![]() 的内角平分线上,则
的内角平分线上,则![]() 长为_______________.
长为_______________.

【答案】3或![]()
【解析】
此题分两种情况:当D点落在∠A的平分线上时,根据角平分线性质特点得DN=DM,进而得出点C,D,N在同一条直线上,再根据已知条件求出CN,证明△MCD![]() △CAN,根据相似比求出CD即可;当D点落在∠B的平分线上时,同理证明出△MCD
△CAN,根据相似比求出CD即可;当D点落在∠B的平分线上时,同理证明出△MCD![]() △NCB,根据相似比求CD.
△NCB,根据相似比求CD.
当D点落在∠A的平分线上时,如图:
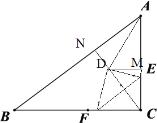
过点D作DN⊥AB,DM⊥AC,
∵AD平分∠BAC,
∴DN=DM,
由对称知识知CD⊥EF,
∵ ![]() ,DN⊥AB,
,DN⊥AB,
∴点C,D,N在同一条直线上,
∵![]() ,
,![]() ,
,![]() ,
,
∴AB=10,
∵![]() 即
即![]() ,
,
∴CN=4.8,
∴AN=![]() =3.6,
=3.6,
∴ DN=DM=4.8-CD,
∵∠CMD=∠ANC,∠MCD=∠CAN,
∴△MCD![]() △CAN,
△CAN,
∴![]() ,
,
即![]() ,
,
解得:CD=3;
当D点落在∠B的平分线上时,如图:
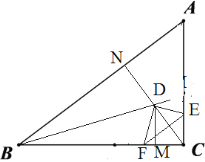
同理:△MCD![]() △NCB,
△NCB,
∴![]()
∴![]() ,
,
即![]() ,
,
解得:CD=![]() ,
,
故答案为:3或![]() .
.


科目:初中数学 来源: 题型:
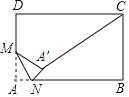
【题目】如图,在矩形ABCD中,AB=12,BC=10,M是AD边的中点,N是AB边上的动点,将△AMN沿MN所在直线折叠,得到△![]() ,连接
,连接![]() ,则
,则![]() 的最小值是__________.
的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O过ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AD交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
(1)求证:△ABH是等腰三角形;
(2)求证:直线PC是⊙O的切线;
(3)若AB=2,AD=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲,乙两个电子团队整理一批电脑数据,整理电脑的台数为![]() (台)与整理需要的时间
(台)与整理需要的时间![]() 之间关系如下图所示,请依据图象提供的信息解答下列问题:
之间关系如下图所示,请依据图象提供的信息解答下列问题:
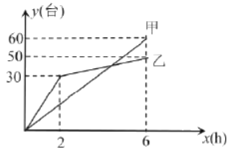
(1)乙队工作![]() 小时整理_____台电脑,工作
小时整理_____台电脑,工作![]() 时两队一共整理了_______台;
时两队一共整理了_______台;
(2)求甲、乙两队![]() 与
与![]() 的关系式.
的关系式.
(3)甲、乙两队整理电脑台数相等时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 为线段
为线段![]() 上一点(不与点
上一点(不与点![]() 、点
、点![]() 重合),连接
重合),连接![]() ,作
,作![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
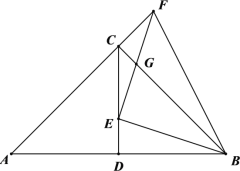
(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在正方形ABCD中,G是CD边上的一个动点(不与C、D重合),以CG为边在正方形ABCD外作一个正方形CEFG,连结BG、DE,如图①.直接写出线段BG、DE的关系 ;
(2)将图①中的正方形CEFG绕点C按顺时针方向旋转任意角度![]() ,如图②,试判断(1)中的结论是否成立?若成立,直接写出结论,若不成立,说明理由;
,如图②,试判断(1)中的结论是否成立?若成立,直接写出结论,若不成立,说明理由;
(3)将(1)中的正方形都改为矩形,如图③,再将矩形CEFG绕点C按顺时针方向旋转任意角度![]() ,如图④,若AB=a,BC=b;CE =ka,CG=kb,(
,如图④,若AB=a,BC=b;CE =ka,CG=kb,(![]() )试判断(1)中的结论是否仍然成立?并说明理由.
)试判断(1)中的结论是否仍然成立?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
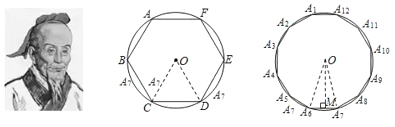
【题目】我国魏晋时期的数学家刘徽(263年左右)首创“割圆术”,所谓“割圆术”就是利用圆内接正多边形无限逼近圆来确定圆周率,刘徽计算出圆周率![]() .刘微从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,…,割得越细,正多边形就越接近圆.设圆的半径为
.刘微从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,…,割得越细,正多边形就越接近圆.设圆的半径为![]() ,圆内接正六边形的周长
,圆内接正六边形的周长![]() ,计算
,计算![]() ;圆内接正十二边形的周长
;圆内接正十二边形的周长![]() ,计算
,计算![]() ;那么分割到圆内接正二十四边形后,通过计算可以得到圆周率
;那么分割到圆内接正二十四边形后,通过计算可以得到圆周率![]() __________.(参考数据:
__________.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,四边形ABCD是正方形,∠MAN=90°,将∠MAN绕顶点A旋转,旋转角为∠DAM(0°<∠DAM<45°),AM交CD于点E,∠MAN的平分线与CB交于点G
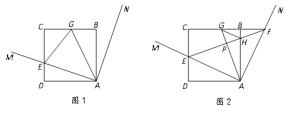
(1)证明:如图1,连接GE.求证:GE=DE+BG;
(2)探究:如图2,设AN交CB的延长线于点F,直线EF分别交AG,AB于点P,H.探究GH与AE的位置关系,并证明你的结论;
(3)应用:在图2中,若正方形的边长为6,BG=2,求GH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com