


 。
。 ,解得
,解得 。
。 ,即
,即 。(2分)
。(2分) ,将A(6,-3)代入得
,将A(6,-3)代入得 ,解得
,解得 。
。 。
。 得y=-2。∴M(4,-2)。
得y=-2。∴M(4,-2)。 。(3分)
。(3分) 于点H,,
于点H,, 与x轴交于点D。则
与x轴交于点D。则 ),
), 。
。 ),N(
),N( ),H(
),H( )。
)。 ,HA=
,HA= ,NH=
,NH= 。
。 。
。
 。∴∠ANM=∠ONM。(2分)
。∴∠ANM=∠ONM。(2分) 。
。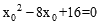 ,解得
,解得 。
。 。
。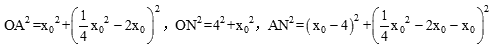 ,
, 。
。 ,解得
,解得 ,
, 。
。 。
。 ,ND=
,ND= ,∴
,∴ 。
。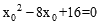 ,解得
,解得 。
。 右侧的二次函数图象上运动时,△ANO不能成为直角三角形。(3分)
右侧的二次函数图象上运动时,△ANO不能成为直角三角形。(3分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=(x-2)2+3 | B.y=(x+2)2+3 | C.y=(x-2)2-3 | D.y=(x+2)2-3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,△AMN的面积为
,△AMN的面积为 .
. 的取值范围.
的取值范围. 的函数.
的函数.


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的正方形并排组成矩形OABC,相邻两边OA、OC分别落在y轴的正半轴和x轴的负半轴上,将这些正方形顺时针绕点O旋转135°得到相应矩形OA′B′C′,二次函数y=ax2+bx(a≠0)过点O、B′、C′.
的正方形并排组成矩形OABC,相邻两边OA、OC分别落在y轴的正半轴和x轴的负半轴上,将这些正方形顺时针绕点O旋转135°得到相应矩形OA′B′C′,二次函数y=ax2+bx(a≠0)过点O、B′、C′.

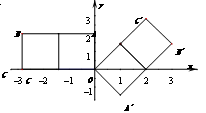
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com