
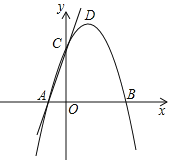
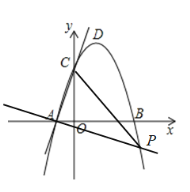
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点C,点D时抛物线的顶点
轴交于点C,点D时抛物线的顶点
(1)求抛物线的解析式和直线![]() 的解析式;
的解析式;
(2)试探究:在抛物线上是否存在点P,使得以点![]() 为顶点,
为顶点,![]() 为直角边的三角形是直角三角形,若存在,请求出,请求出符合条件的点P的坐标;若不存在,请说明理由.
为直角边的三角形是直角三角形,若存在,请求出,请求出符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;直线AC的方程为
;直线AC的方程为![]() ;(2)存在,点P的坐标为
;(2)存在,点P的坐标为![]() 或
或![]() .
.
【解析】
(1)根据抛物线与![]() 的交点坐标
的交点坐标![]() ,设抛物线的解析式为
,设抛物线的解析式为![]() ,化简得
,化简得![]() ,与原题的解析式对比,易得
,与原题的解析式对比,易得![]() ,解出a的值,代入所设解析式即可得抛物线解析式;
,解出a的值,代入所设解析式即可得抛物线解析式;
根据抛物线与![]() 轴交于点C,可求得
轴交于点C,可求得![]() ,设直线AC的解析式为
,设直线AC的解析式为![]() ,把A、C的坐标代入可求出
,把A、C的坐标代入可求出![]() ,从而即可求得直线AC的解析式;
,从而即可求得直线AC的解析式;
(2)分两种情况求解:①过点C作AC的垂线交抛物线于另一点P,则直线PC的解析式为![]() ,再联立
,再联立![]() ,可求得交点P的坐标为
,可求得交点P的坐标为![]() ;
;
②过点A作AC的垂线交抛物线于点P,则可得所以直线PC的解析式为![]() ,联立
,联立![]() ,可求得点P的坐标为
,可求得点P的坐标为![]() .
.
解:(1)设抛物线的解析式为![]() ,
,
![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
所以抛物线的解析式为![]() ;
;
当![]() 时,
时, ![]() ,
,
∴![]() ;
;
设直线AC的解析式为![]() ,
,
把![]() 代入,
代入, ![]() ,
,
所以![]() ,
,
所以直线AC的方程为![]() ;
;
(2)存在;理由如下:
①过点C作AC的垂线交抛物线于另一点P,
∵直线AC的方程为![]() ,
,
∴直线PC的解析式为![]() ,
,
解方程组: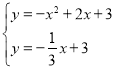 ,
,
解得:![]() 或
或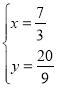 ,
,
此时点P的坐标为![]() ;
;
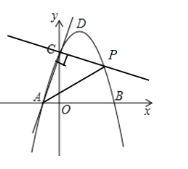
②过点A作AC的垂线交抛物线于点P,
直线PC的解析式为![]() ,
,
把![]() 代入得
代入得![]() ,
,
所以直线PC的解析式为![]() ,
,
解方程组: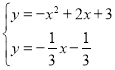 ,
,
解得:![]() 或
或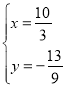 ,
,
所以点P的坐标为![]() .
.
综上所述,符合条件的点P的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正确的是( )
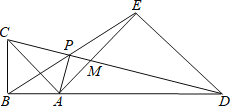
A. ①②B. ①②③C. ①②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a∥b,∠1=40°,∠2=80°,则∠3的度数为( )
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/15/2485292109684736/2491850430775296/STEM/0502255e02c3498e9234cb6eaef26eb9.png]
A.120°B.130°C.140°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的菱形ABCD中,对角线AC,BD交点与点O,点P是△ADO的重心.
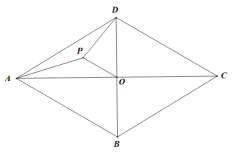
(1)当菱形ABCD是正方形时,则PA=________,PD=__________,PO=_________.
(2)线段PA,PD,PO中是否存在长度保持不变的线段,若存在,请求出该线段的长度,若不存在,请说明理由.
(3)求线段PD,DO满足的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() .折叠该纸片,使点
.折叠该纸片,使点![]() 落在线段
落在线段![]() 上,折痕与边
上,折痕与边![]() 交于点
交于点![]() ,与边
,与边![]() 交于点
交于点![]() .
.
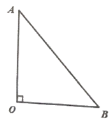
(1)若折叠后使点![]() 与点
与点![]() 重合,此时
重合,此时![]() __________;
__________;
(2)若折叠后使点![]() 与边
与边![]() 的中点重合,求
的中点重合,求![]() 的长度;
的长度;
(3)若折叠后点![]() 落在边
落在边![]() 上的点为
上的点为![]() ,且使
,且使![]() ,求此时
,求此时![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
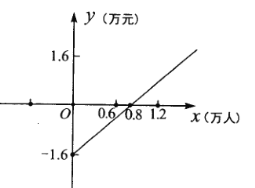
【题目】某公共汽车线路每天运营毛利润![]() (万元)与乘客量
(万元)与乘客量![]() (万人)成一次函数关系,其图象如图所示.目前通过监测发现每天平均乘客量为0.6万人次,由于运营成本较高,这条线路处于亏损状态.(毛利润=票价总收入一运营成本)
(万人)成一次函数关系,其图象如图所示.目前通过监测发现每天平均乘客量为0.6万人次,由于运营成本较高,这条线路处于亏损状态.(毛利润=票价总收入一运营成本)
(1)求该线路公共汽车的单程票价和每天运营成本分别为多少元.
(2)公交公司为了扭亏,若要使每天运营毛利润在0.2~0.4万元之间(包括0.2和0.4),求平均每天的乘客量![]() 的范围.
的范围.
(3)据实际情况,发现该线路乘客量稳定,公交公司决定适当提高票价,当单程票价每提高1元时,每天平均乘客量相应减少0.05万人次,设这条线路的单程票价提高![]() 元(
元(![]() ).当
).当![]() 为何值时,该线路每天运营总利润最大,并求出最大的总利润.
为何值时,该线路每天运营总利润最大,并求出最大的总利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
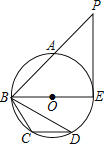
【题目】如图,已知A、B、C、D、E是⊙O上五点,⊙O的直径BE=2![]() ,∠BCD=120°,A为
,∠BCD=120°,A为![]() 的中点,延长BA到点P,使BA=AP,连接PE.
的中点,延长BA到点P,使BA=AP,连接PE.
(1)求线段BD的长;
(2)求证:直线PE是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com