
【题目】某学校举行“青春心向党建功新时代”演讲比赛活动,准备购买甲、乙两种奖品,小昆发现用480元购买甲种奖品的数目恰好与用360元购买乙种奖品的数目相等,已知甲种奖品的单价比乙种奖品的单价多10元.
(1)求甲、乙两种奖品的单价各是多少元?
(2)如果需要购买甲乙两种奖品共100个,且甲种奖品的数目不低于乙种奖品数目的2倍,问购买多少个甲种奖品,才使得总购买费用最少?
【答案】(1) 甲种奖品的单价为40元,乙种奖品的单价为30元;(2)购买甲种奖品67个时,总费用最少
【解析】
(1)设甲种奖品的单价为![]() 元,则乙种奖品的单价为
元,则乙种奖品的单价为![]() 元,利用“480元购买甲种奖品的数目恰好与用360元购买乙种奖品的数目相等”为等量关系列方程求解即可;
元,利用“480元购买甲种奖品的数目恰好与用360元购买乙种奖品的数目相等”为等量关系列方程求解即可;
(2)设购买甲种奖品![]() 个,则购买乙种奖品
个,则购买乙种奖品![]() 个,购买奖品的总费用为w元,由甲种奖品的数目不低于乙种奖品数目的2倍可得出关于m的一元一次不等式,解之即可得出m的取值范围,根据总价=单价×数量可得出w关于m的一次函数关系式,再利用一次函数的性质即可解决最值问题.
个,购买奖品的总费用为w元,由甲种奖品的数目不低于乙种奖品数目的2倍可得出关于m的一元一次不等式,解之即可得出m的取值范围,根据总价=单价×数量可得出w关于m的一次函数关系式,再利用一次函数的性质即可解决最值问题.
(1)设甲种奖品的单价为![]() 元,则乙种奖品的单价为
元,则乙种奖品的单价为![]() 元.
元.
由题意得![]() ,
,
解得![]() ,
,
经检验得![]() 是原方程的解,
是原方程的解,
∴![]() ,
,
答:甲种奖品的单价为40元,乙种奖品的单价为30元;
(2)设购买甲种奖品![]() 个,则购买乙种奖品
个,则购买乙种奖品![]() 个,
个,
由题意得:![]()
解得:![]() ;
;
∵![]() 取正整数;
取正整数;
∴![]() ;
;
设购买奖品的总费用为w元,
由题意得:![]() ,
,
即![]() ,
,
∵![]() ,
,
∴![]() 随
随![]() 的增大而增大,
的增大而增大,
∴![]() 时,
时,![]() 最小;
最小;
答:购买甲种奖品67个时,总费用最少.


科目:初中数学 来源: 题型:
【题目】中央电视台的《朗读者》节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数量少的有![]() 本,最多的有
本,最多的有![]() 本,并根据调查结果绘制了不完整的图表,如下所示:
本,并根据调查结果绘制了不完整的图表,如下所示:
本数(本) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|

(![]() )统计图表中的
)统计图表中的![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(![]() )请将频数分布直方图补充完整.
)请将频数分布直方图补充完整.
(![]() )求所有被调查学生课外阅读的平均本数.
)求所有被调查学生课外阅读的平均本数.
(![]() )若该校八年级共有
)若该校八年级共有![]() 名学生,请你估计该校八年级学生课外阅读
名学生,请你估计该校八年级学生课外阅读![]() 本及以上的人数.
本及以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
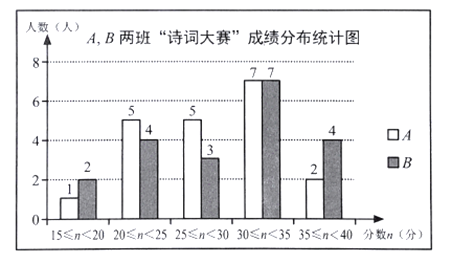
【题目】为让学生感受中华诗词之美,某校九年级举行了“诗词大赛”,为了解九年级![]() 两班学生的“诗词大赛”成绩,分别从每班
两班学生的“诗词大赛”成绩,分别从每班![]() 名学生中各随机抽取
名学生中各随机抽取![]() 人的“诗词大赛”成绩(满分为
人的“诗词大赛”成绩(满分为![]() 分,成绩均为整数),制成如图所示的统计图.
分,成绩均为整数),制成如图所示的统计图.
![]() 若将不低于
若将不低于![]() 分的成绩评为优秀,请你估计一下哪个班级优秀人数多? 多几人?
分的成绩评为优秀,请你估计一下哪个班级优秀人数多? 多几人?
![]() 请你选择适当的统计量来说明
请你选择适当的统计量来说明![]() 两班哪个班级的整体成绩较好?
两班哪个班级的整体成绩较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究发现,二次函数![]() (
(![]() )图象上任何一点到定点(0,
)图象上任何一点到定点(0,![]() )和到定直线
)和到定直线![]() 的距离相等.我们把定点(0,
的距离相等.我们把定点(0,![]() )叫做抛物线
)叫做抛物线![]() 的焦点,定直线
的焦点,定直线![]() 叫做抛物线
叫做抛物线![]() 的准线.
的准线.
(1)写出函数![]() 图象的焦点坐标和准线方程;
图象的焦点坐标和准线方程;
(2)等边三角形OAB的三个顶点都在二次函数![]() 图象上,O为坐标原点,求等边三角形的边长;
图象上,O为坐标原点,求等边三角形的边长;
(3)M为抛物线![]() 上的一个动点,F为抛物线
上的一个动点,F为抛物线![]() 的焦点,P(1,3)为定点,求MP+MF的最小值.
的焦点,P(1,3)为定点,求MP+MF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠A=90°,∠B=30°,CD=CA,D在BC上,∠ADE=45°,E在AB上,则∠BED的度数是( )
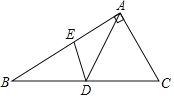
A.60°B.75°C.80°D.85°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表显示的是某种大豆在相同条件下的发芽试验结果:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n为400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率是0.955;
②随着试验时大豆的粒数的增加,大豆发芽的频率总在0.95附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是0.95;
③若大豆粒数n为4000,估计大豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ①②③ B. ①② C. ①③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
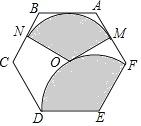
【题目】如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com