
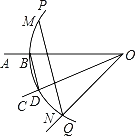
【题目】如图:已知锐角∠AOC,依次按照以下顺序操作画图:
(1)在射线OA上取一点B,以点O为圆心,OB长为半径作![]() ,交射线OC于点D,连接BD;
,交射线OC于点D,连接BD;
(2)分别以点B,D为圆心,BD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接ON,MN.
根据以上作图过程及所作图形可知下列结论:①OC平分∠AON;②MN∥BD;③MN=3BD;④若∠AOC=30°,则MN=![]() ON.其中正确结论的序号是_____.
ON.其中正确结论的序号是_____.
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知二次函数
中,已知二次函数![]() 的图象与x轴交于点
的图象与x轴交于点![]() ,与y轴交于点B,将其图象在点A,B之间的部分(含A,B两点)记为F.
,与y轴交于点B,将其图象在点A,B之间的部分(含A,B两点)记为F.
(1)求点B的坐标及该函数的表达式;
(2)若二次函数![]() 的图象与F只有一个公共点,结合函数图象,求a的取值范围.
的图象与F只有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个点的纵坐标是横坐标的二倍,则称该点为“倍点”
(1)若点![]() 是双曲线
是双曲线![]() 上的倍点,则
上的倍点,则![]() ;
;
(2)求出直线![]() 上的倍点的坐标;
上的倍点的坐标;
(3)若抛物线![]() 上有且只有一个倍点,求
上有且只有一个倍点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】云岗石窟位于山西大同市,是中国规模最大的古代石窟群之一,位于第五窟的三世佛的中央坐像是云冈石窟最大的佛像.某数学课题研究小组针对“三世佛的中央坐像的高度有多少米”这一问题展开探究,过程如下:

问题提出:
如图①是三世佛的中央坐像,请你设计方案并求出它的高度.
方案设计:
如图②,该课题研究小组通过研究设计了这样一个方案,某同学在![]() 处用测角器测得佛像最高处
处用测角器测得佛像最高处![]() 的仰角
的仰角![]() ,另一个同学在他的后方
,另一个同学在他的后方![]() 的
的![]() 处测得佛像底端
处测得佛像底端![]() 的仰角
的仰角![]() .
.
数据收集:
通过查阅资料和实际测量:佛像底端到观景台的垂直距离![]() 为
为![]() .
.
问题解决:
(1)根据上述方案及数据,求佛像![]() 的高度;(结果保留整数,参考数据:
的高度;(结果保留整数,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
(2)在实际测量的过程中,有哪些措施可以减小测量数据产生的误差?(写出一条即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
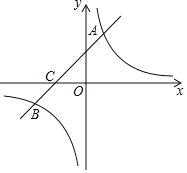
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于第一、三象限内的
的图象相交于第一、三象限内的![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
⑴求该反比例函数和一次函数的解析式;
⑵在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最大,求
最大,求![]() 的最大值及点
的最大值及点![]() 的坐标;
的坐标;
⑶直接写出当![]() 时,
时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
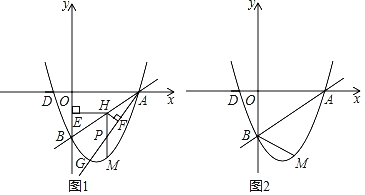
【题目】如图,一次函数y=![]() x﹣2的图象与x轴交于点A,与y轴交于点B,点D的坐标为(﹣1,0),二次函数y=ax2+bx+c(a≠0)的图象经过A,B,D三点.
x﹣2的图象与x轴交于点A,与y轴交于点B,点D的坐标为(﹣1,0),二次函数y=ax2+bx+c(a≠0)的图象经过A,B,D三点.
(1)求二次函数的解析式;
(2)如图1,已知点G(1,m)在抛物线上,作射线AG,点H为线段AB上一点,过点H作HE⊥y轴于点E,过点H作HF⊥AG于点F,过点H作HM∥y轴交AG于点P,交抛物线于点M,当HEHF的值最大时,求HM的长;
(3)在(2)的条件下,连接BM,若点N为抛物线上一点,且满足∠BMN=∠BAO,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
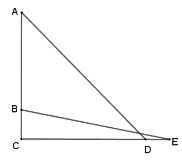
【题目】如图1.在![]() 中,
中,![]() 把
把![]() 沿对角线
沿对角线![]() 所在的直线折叠,使点
所在的直线折叠,使点![]() 落在点
落在点![]() 处,
处,![]() 交
交![]() 于点
于点![]() .连接
.连接![]() .
.

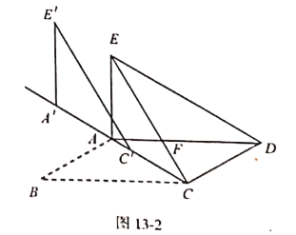
(1)求证:![]() ;
;
(2)求证:![]() 为等腰三角形;
为等腰三角形;
(3)将图1中![]() 的沿射线
的沿射线![]() 方向平移得到
方向平移得到![]() (如图2所示) .若在
(如图2所示) .若在![]() 中,
中,![]() . 当
. 当![]() 时,直接写出
时,直接写出![]() 平移的距离.
平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
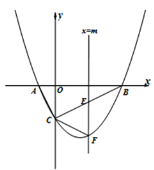
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y=
与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y=![]() x-2,作垂直于x轴的直线
x-2,作垂直于x轴的直线![]() ,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).
,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).
(1)求抛物线的解析式;
(2)若△CEF是以CE为腰的等腰三角形,求m的值;
(3)点P为y轴左侧抛物线上的一点,过点P作![]() 交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.
交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有甲、乙两座楼房,楼间距BC为50米,在乙楼顶部A点测得甲楼顶部D点的仰角为37°,在乙楼底部B点测得甲楼顶部D点的仰角为60°,则甲、乙两楼的高度分别为多少?(结果精确到1米,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com