
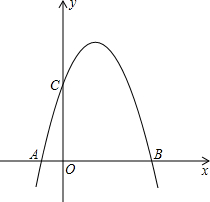 已知:如图,抛物线
已知:如图,抛物线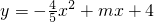 与y轴交于点C,与x轴交于点A、B,(点A在点B的左侧)且满足OC=4OA.设抛物线的对称轴与x轴交于点M:
与y轴交于点C,与x轴交于点A、B,(点A在点B的左侧)且满足OC=4OA.设抛物线的对称轴与x轴交于点M: x2+mx+4得,-
x2+mx+4得,- ×(-1)2+m×(-1)+4=0,
×(-1)2+m×(-1)+4=0, ,
, x2+
x2+ x+4,
x+4, =2,
=2, =2
=2 ,
, x2+
x2+ x+4=0,
x+4=0, =
=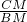 ,
,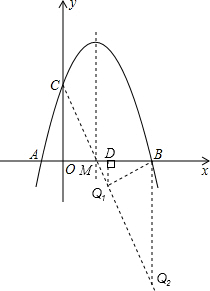
 =
=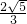 ,
, ,
, ×
× =
= ,QD=BQ•sin∠QBM=
,QD=BQ•sin∠QBM= ×
× =
= ,
, =
=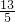 ,
,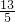 ,-
,- ),
), ,
, ,
, x-
x- ;
; =
=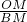 ,
, =
= ,
, ,
, ,
, x-
x- 或y=-x-1.
或y=-x-1.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
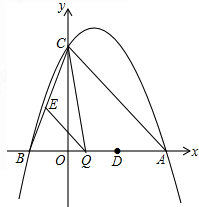 (2012•浦江县模拟)已知:如图,抛物线与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0),点B的坐标为(-2,0).
(2012•浦江县模拟)已知:如图,抛物线与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0),点B的坐标为(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,点
,点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
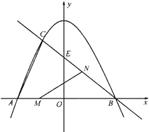
(1)写出直线![]() 的解析式.
的解析式.
(2)求![]() 的面积.
的面积.
(3)若点![]() 在线段
在线段![]() 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从![]() 向
向![]() 运动(不与
运动(不与![]() 重合),同时,点
重合),同时,点![]() 在射线
在射线![]() 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从![]() 向
向![]() 运动.设运动时间为
运动.设运动时间为![]() 秒,请写出
秒,请写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并求出点
的函数关系式,并求出点![]() 运动多少时间时,
运动多少时间时,![]() 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
 与
与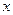 轴交于点
轴交于点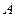 、点
、点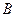 ,与直线
,与直线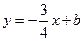 相交于点
相交于点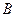 、点
、点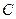 ,直线
,直线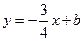 与
与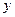 轴交于点
轴交于点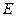 。
。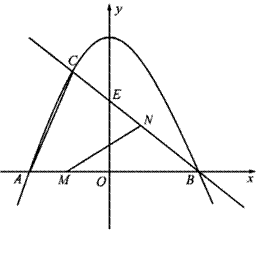
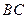 的解析式;
的解析式;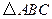 的面积;
的面积;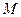 在线段
在线段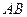 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从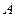 向
向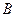 运动(不与
运动(不与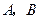 重合),同时,点
重合),同时,点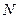 在射线
在射线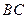 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从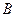 向
向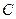 运动.设运动时间为
运动.设运动时间为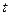 秒,请写出
秒,请写出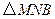 的面积
的面积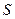 与
与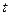 的函数关系式,并求出点
的函数关系式,并求出点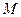 运动多少时间时,
运动多少时间时,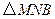 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京师大附中九年级上学期期中考试数学卷 题型:解答题
已知:如图,抛物线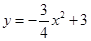 与
与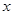 轴交于点
轴交于点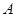 ,点
,点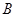 ,与直线
,与直线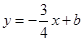 相交于点
相交于点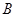 ,点
,点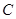 ,直线
,直线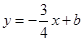 与
与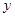 轴交于点
轴交于点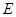 .
.
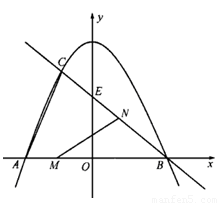
1.(1)求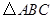 的面积.
的面积.
2.(2)若点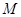 在线段
在线段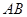 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从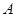 向
向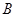 运动(不与
运动(不与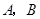 重合),同时,点
重合),同时,点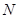 在射线
在射线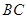 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从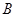 向
向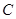 运动.设运动时间为
运动.设运动时间为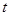 秒,请写出
秒,请写出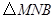 的面积
的面积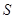 与
与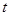 的函数关系式,并求出点
的函数关系式,并求出点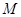 运动多少时间时,
运动多少时间时,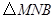 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源:2013届河南省周口市初一下学期第九章一元一次不等式组检测题 题型:解答题
已知:如图,抛物线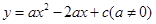 与
与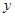 轴交于点
轴交于点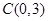 ,与
,与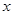 轴交于
轴交于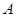 、
、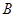 两点,点
两点,点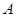 的坐标为
的坐标为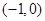 .
.
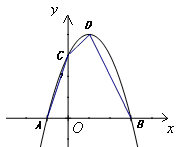
(1)求抛物线的解析式及顶点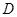 的坐标;
的坐标;
(2)设点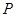 是在第一象限内抛物线上的一个动点,求使与四边形
是在第一象限内抛物线上的一个动点,求使与四边形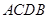 面积相等的四边形
面积相等的四边形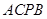 的点
的点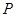 的坐标;
的坐标;
(3)求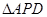 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com