
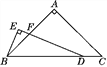
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D在线段BC上,∠EDB=![]() ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.
【答案】BE=![]() DF
DF
【解析】试题分析:BE与DH的延长线交于G点,由DH∥AC得到∠BDH=45°,则△HBD为等腰直角三角形,于是HB=HD,由∠EBF=22.5°得到DE平分∠BDG,
根据等腰三角形性质得BE=GE,即BE=![]() BG,然后根据“AAS”证明△BGH≌△DFH,则BG=DF,所以BE=
BG,然后根据“AAS”证明△BGH≌△DFH,则BG=DF,所以BE=![]() FD.
FD.
试题解析:
BE=![]() FD.理由:
FD.理由:
BE与DH的延长线交于G点,如图所示:
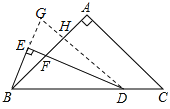
∵DH∥AC,
∴∠BDH=∠C=45°,
∴△HBD为等腰直角三角形
∴HB=HD,
而∠EBF=22.5°,
∵∠EDB=![]() ∠C=22.5°,
∠C=22.5°,
∴DE平分∠BDG,
而DE⊥BG,
∴BE=GE,即BE=![]() BG,
BG,
∵∠DFH+∠FDH=∠G+∠FDH=90°,
∴∠DFH=∠G,
∵∠GBH=90°-∠G,∠FDH=90°-∠G,
∴∠GBH=∠FDH
在△BGH和△DFH中,
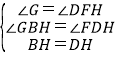
∴△BGH≌△DFH(AAS),
∴BG=DF,
∴BE=![]() FD.
FD.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() .
.
![]() 求证:抛物线总与
求证:抛物线总与![]() 轴有两个不同的交点;
轴有两个不同的交点;
![]() 若
若![]() ,求此抛物线的解析式.
,求此抛物线的解析式.
![]() 已知
已知![]() 轴上两点
轴上两点![]() ,
,![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有交点,请写出
有交点,请写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ABC=90°,AB=BC,点A,B分别在坐标轴上.
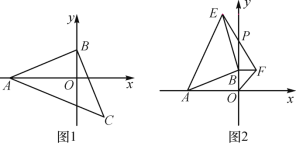
(1)如图1,若点C的横坐标为5,直接写出点B的坐标 ;
(2)如图2,若点A的坐标为(-6,0),点B在y轴的正半轴上运动时,分别以OB,AB为边在第一、第二象限作等腰Rt△OBF,等腰Rt△ABE,连接EF交y轴于点P,当点B在y轴的正半轴上移动时,PB的长度是否发生改变?若不变,求出PB的值;若变化,求PB的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,直线AB交
中,直线AB交![]() 轴于A(2,0),交
轴于A(2,0),交![]() 轴负半轴于B(0,-10),C为x轴正半轴上一点,且OC=5OA.
轴负半轴于B(0,-10),C为x轴正半轴上一点,且OC=5OA.
(1)求△ABC的面积.
(2)延长BA到P(自己补全图形),使得PA=AB,过点P作PM⊥OC于M,求P点的坐标.
(3)如图,D是第三象限内一动点,直线BE⊥CD于E, OF⊥OD交BE延长线于F.当D点运动时,![]() 的大小是否发生变化?若改变,请说明理由;若不变,求出这个比值.
的大小是否发生变化?若改变,请说明理由;若不变,求出这个比值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区对![]() 个旅游景点的游客人数进行了统计,有关数据如下表:
个旅游景点的游客人数进行了统计,有关数据如下表:
景点 |
|
|
|
|
|
票价(元) |
|
|
|
|
|
平均日人数(千人) |
|
|
|
|
|
![]() 如果这个星期天你去此风景区游玩,小刚、小明也去了,你在哪个景点遇见他们两个的机会较大?为什么?
如果这个星期天你去此风景区游玩,小刚、小明也去了,你在哪个景点遇见他们两个的机会较大?为什么?
![]() 如果到了这个风景区,你不想把这几个景点全部参观完,但又不知选哪一个,于是你想出一个主意:抓阄,那么,你抓出哪种票价的机会较大有多大?此时你参观哪个景点的机会较大?
如果到了这个风景区,你不想把这几个景点全部参观完,但又不知选哪一个,于是你想出一个主意:抓阄,那么,你抓出哪种票价的机会较大有多大?此时你参观哪个景点的机会较大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2:按上述方法不断操作下去…,经过第2019次操作后得到的折痕D2018E2018,到BC的距离记为h2019:若h1=1,则h2019的值为(____)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒1 cm的速度沿折线
出发,以每秒1 cm的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒(
秒(![]() >0).
>0).

(1)若点![]() 在
在![]() 上,且满足
上,且满足![]() ,求此时
,求此时![]() 的值;
的值;
(2)若点![]() 恰好在
恰好在![]() 的角平分线上,求此时
的角平分线上,求此时![]() 的值;
的值;
(3)在运动过程中,当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设m是不小于﹣1的实数,关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有两个不相等的实数根x1、x2,
(1)若x12+x22=6,求m值;
(2)令T=![]() ,求T的取值范围.
,求T的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com