
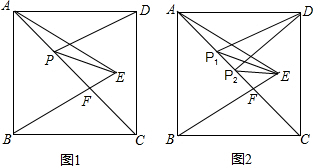
 存在,请说明理由;若存在,请说出这个最小值,并证明你的结论.
存在,请说明理由;若存在,请说出这个最小值,并证明你的结论.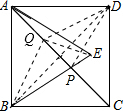
| 3 |
| 3 |
| 3 |
| 3 |


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
 AF=BD.
AF=BD.查看答案和解析>>
科目:初中数学 来源: 题型:
 三视图如图2所示,则增加的两个正方体放在( )
三视图如图2所示,则增加的两个正方体放在( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2011•蜀山区二模)如图所示,在高速公路紧靠护栏外的点A处观测公路对面护栏外一点C,测得C在点A北偏东63°的方向上;沿护栏前行60米到达B处,测得C在点B北偏东45°的方向上,根据以上数据,计算这条高速公路的宽度(含公路中间的隔离带).(参考数值:tan63°≈2,tan27°≈
(2011•蜀山区二模)如图所示,在高速公路紧靠护栏外的点A处观测公路对面护栏外一点C,测得C在点A北偏东63°的方向上;沿护栏前行60米到达B处,测得C在点B北偏东45°的方向上,根据以上数据,计算这条高速公路的宽度(含公路中间的隔离带).(参考数值:tan63°≈2,tan27°≈| 1 |
| 2 |
| 9 |
| 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:
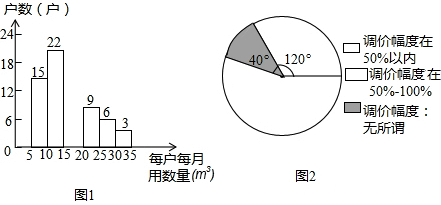
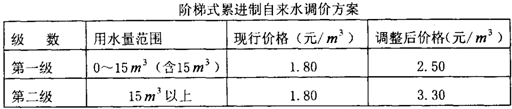
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com