
【题目】根据绝对值定义,若有![]() ,则
,则![]() 或
或![]() ,若
,若![]() ,则
,则![]() ,我们可以根据这样的结论,解一些简单的绝对值方程,例如:
,我们可以根据这样的结论,解一些简单的绝对值方程,例如:![]()
解:方程![]() 可化为:
可化为:
![]() 或
或![]()
当![]() 时, 则有:
时, 则有:![]() ; 所以
; 所以 ![]() .
.
当![]() 时, 则有:
时, 则有:![]() ;所以
;所以 ![]() .
.
故,方程![]() 的解为
的解为![]() 或
或![]() 。
。
(1)解方程:![]()
(2)已知![]() ,求
,求![]() 的值;
的值;
(3)在 (2)的条件下,若![]() 都是整数,则
都是整数,则![]() 的最大值是 (直接写结果,不需要过程).
的最大值是 (直接写结果,不需要过程).
科目:初中数学 来源: 题型:
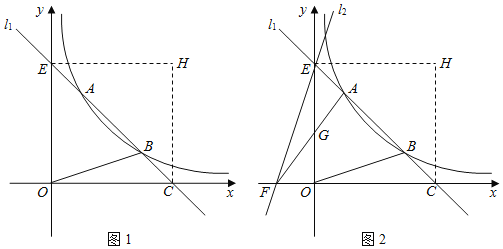
【题目】如图1,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 、点
、点![]() .
.
(1)求直线![]() 和双曲线的解析式;
和双曲线的解析式;
(2)将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在第一象限内的点
落在第一象限内的点![]() 处,直接写出点
处,直接写出点![]() 的坐标;
的坐标;
(3)如图2,过点![]() 作直线
作直线![]() 交
交![]() 轴的负半轴于点
轴的负半轴于点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.
①求直线![]() 的解析式;
的解析式;
②在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,请直接写出所有符合条件的点
?若存在,请直接写出所有符合条件的点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为预防传染病,某校定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量 ![]() 与药物在空气中的持续时间
与药物在空气中的持续时间![]() 成正比例;燃烧后,
成正比例;燃烧后,![]() 与
与![]() 成反比例(如图所示).现测得药物
成反比例(如图所示).现测得药物![]() 分钟燃完,此时教室内每立方米空气含药量为
分钟燃完,此时教室内每立方米空气含药量为![]() .根据以上信息解答下列问题:
.根据以上信息解答下列问题:
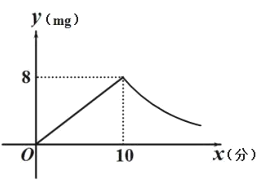
(1)分别求出药物燃烧时及燃烧后 ![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)当每立方米空气中的含药量低于![]() 时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
(3)当室内空气中的含药量每立方米不低于![]() 的持续时间超过
的持续时间超过![]() 分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.
分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
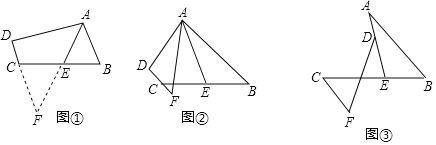
【题目】(1)阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB、AD、DC之间的等量关系为 ;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
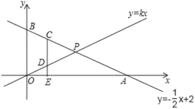
【题目】在平面直角坐标系中,一次函数![]() 的图象交
的图象交![]() 轴、
轴、![]() 轴分别于
轴分别于![]() 两点,交直线
两点,交直线![]() 于
于![]() 。
。
(1)求点![]() 的坐标;
的坐标;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,![]() 是线段
是线段![]() 上一点,
上一点,![]() 轴于
轴于![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 点的坐标。
点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中,装有2个红球,1个白球,1个黄球,这些球除颜色外都相同.求下列事件的概率:
(1)搅匀后从中任意摸出1个球,恰好是红球;
(2)搅匀后从中任意摸出2个球,2个都是红球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华将一条直角边长为1的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到一个等腰直角三角形(如图3),则图3中的等腰直角三角形的一条腰长为_________;同上操作,若小华连续将图1的等腰直角三角形折叠n次后所得到的等腰直角三角形(如图n+1)的一腰长为_________.
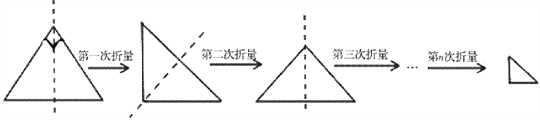
图1 图2 图3 图n+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com