
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
【答案】(1)12万元和10万元.(2)有6种购买方案.
(3)最省钱的购买方案为,选购甲型设备4台,乙型设备6台
【解析】试题分析:(1)设甲,乙两种型号设备每台的价格分别为![]() 万元和
万元和![]() 万元,根据购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.列出方程组,求出
万元,根据购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.列出方程组,求出![]() 的值即可得出答案;
的值即可得出答案;
(2)设节省能源的新设备甲型设备![]() 台,乙型设备
台,乙型设备![]() 台,根据该公司购买节能设备的资金不超过110万元,列出不等式,求出
台,根据该公司购买节能设备的资金不超过110万元,列出不等式,求出![]() 的值即可得出答案;
的值即可得出答案;
(3)因为公司要求每月的产量不低于2040吨,得出![]() 解之求出
解之求出![]() 的值,确定出方案,然后进行比较即可.
的值,确定出方案,然后进行比较即可.
试题解析:(1)设甲,乙两种型号设备每台的价格分别为![]() 万元和
万元和![]() 万元,
万元,
由题意得: ![]() 解得
解得![]()
∴甲,乙两种型号设备每台的价格分别为12万元和10万元.
(2)设购买甲型设备![]() 台,乙型设备
台,乙型设备![]() 台,
台,
则: ![]()
![]()
∵![]() 取非负整数
取非负整数
∴![]() =0,1,2,3,4,5,
=0,1,2,3,4,5,
∴ 有6种购买方案.
![]() 由题意:
由题意: ![]()
∴![]()
∴![]() 为4或5.
为4或5.
当![]() =4时,购买资金为:12×4+10×6=108(万元),
=4时,购买资金为:12×4+10×6=108(万元),
当![]() =5时,购买资金为:12×5+10×5=110(万元),
=5时,购买资金为:12×5+10×5=110(万元),
∴最省钱的购买方案为,选购甲型设备4台,乙型设备6台


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=6,OC=4,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数 ![]() 的图象与BC边交于点E.
的图象与BC边交于点E.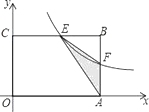
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图①,在正方形ABCD中,点P在边CD上(不与点C、D重合),连接BP,将△BCP绕点C顺时针旋转至△DCE,点B的对应点是点D.旋转的角度是 度.应用:将图①中的BP延长交边DE于点F,其它条件不变,如图②,求∠BFE的度数。拓展:如图②,若DP=2CP,BC=6,则四边形ABED的面积是 .
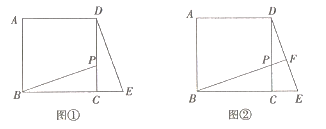
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
(1)有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.例如:![]() 的有理化因式是
的有理化因式是![]() ;
;![]() 的有理化因式是
的有理化因式是![]() .
.
(2)分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到去分母中根号的目的.如:![]() ,
,![]()
问题解决:
(1)填空:![]() 的有理化因式是______.(x≥1)
的有理化因式是______.(x≥1)
(2)直接写出下列各式分母有理化的结果:
①![]() _____;②
_____;②![]() ______.
______.
(3)计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个一次函数与![]() 轴的交点关于
轴的交点关于![]() 轴对称,则称这两个一次函数为“对心函数”,这两个与
轴对称,则称这两个一次函数为“对心函数”,这两个与![]() 轴的交点为“对心点”.
轴的交点为“对心点”.

(1)写出一个![]() 的对心函数:________,这两个“对心点”为:_______;
的对心函数:________,这两个“对心点”为:_______;
(2)直线![]() 经过点
经过点![]() 和
和![]() ,直线
,直线![]() 的“对心函数”直线
的“对心函数”直线![]() 与
与![]() 轴的交点
轴的交点![]() 位于点
位于点![]() 的上方,且直线
的上方,且直线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() 为直线
为直线![]() 的“对心点”.点
的“对心点”.点![]() 是动直线
是动直线![]() 上不与
上不与![]() 重合的一个动点,且
重合的一个动点,且![]() ,试探究
,试探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)如图,直线![]() 与其“对心函数”直线
与其“对心函数”直线![]() 的交点
的交点![]() 位于第一象限,
位于第一象限,![]() 、
、![]() 分别为直线
分别为直线![]() 、
、![]() 的“对心点”,点
的“对心点”,点![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() ;一动点
;一动点![]() 从
从![]() 出发,沿线段
出发,沿线段![]() 以
以![]() 单位
单位![]() 秒的速度运动到点
秒的速度运动到点![]() ,再沿线段
,再沿线段![]() 以
以![]() 单位
单位![]() 秒的速度运动到点
秒的速度运动到点![]() 后停止,点
后停止,点![]() 在整个运动过程中所用最短时间为
在整个运动过程中所用最短时间为![]() 秒,求直线
秒,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com