
【题目】如图,已知![]() 于
于![]() ,
,![]() 于
于![]() ,要计算
,要计算![]() ,
,![]() 两地的距离,甲、乙、丙、丁四组同学分别测量了部分线段的长度和角的度数,得到以下四组数据:甲:
两地的距离,甲、乙、丙、丁四组同学分别测量了部分线段的长度和角的度数,得到以下四组数据:甲:![]() ,
,![]() ;乙:
;乙:![]() ,
,![]() ,
,![]() ;丙:
;丙:![]() 和
和![]() ;丁:
;丁:![]() ,
,![]() ,
,![]() .其中能求得
.其中能求得![]() ,
,![]() 两地距离的有( )
两地距离的有( )

A. 1组 B. 2组 C. 3组 D. 4组
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(11·贵港)如图所示,正方形OEFG和正方形ABCD是位似图形,点F的坐标
为(-1,1),点C的坐标为(-4,2),则这两个正方形位似中心的坐标是 _ ▲ .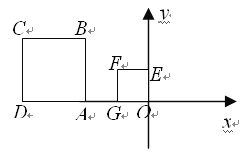
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 为等边三角形,点
为等边三角形,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 、
、![]() 重合).以
重合).以![]() 为边作菱形
为边作菱形![]() ,使
,使![]() ,连接
,连接![]() .
.
![]() 如图
如图![]() ,当点
,当点![]() 在边
在边![]() 上时,
上时,
①求证:![]() ;②请直接判断结论
;②请直接判断结论![]() 是否成立;
是否成立;
![]() 如图
如图![]() ,当点
,当点![]() 在边
在边![]() 的延长线上时,其他条件不变,结论
的延长线上时,其他条件不变,结论![]() 是否成立?请写出
是否成立?请写出![]() 、
、![]() 、
、![]() 之间存在的数量关系,并写出证明过程;
之间存在的数量关系,并写出证明过程;
![]() 如图
如图![]() ,当点
,当点![]() 在边
在边![]() 的延长线上时,且点
的延长线上时,且点![]() 、
、![]() 分别在直线
分别在直线![]() 的异侧,其他条件不变,请补全图形,并直接写出
的异侧,其他条件不变,请补全图形,并直接写出![]() 、
、![]() 、
、![]() 之间存在的等量关系.
之间存在的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BA=BC,BD是三角形的角平分线,DE∥BC交AB于E,下列结论:①∠1=∠3;②![]() ;③
;③![]() 。正确的有__________。(填序号)
。正确的有__________。(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为![]() 米的竹竿的影长为
米的竹竿的影长为![]() 米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为
米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为![]() 米,一级台阶高为
米,一级台阶高为![]() 米,如图所示,若此时落在地面上的影长为
米,如图所示,若此时落在地面上的影长为![]() 米,则树高为( )
米,则树高为( )

A. 11.5米 B. 11.75米 C. 11.8米 D. 12.25米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】测量物体高度
![]() 小明想测量一棵树的高度
小明想测量一棵树的高度![]() ,在阳光下,小明测得一根长为
,在阳光下,小明测得一根长为![]() 米的竹竿的影长为
米的竹竿的影长为![]() 米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为
米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为![]() 米,落在地面上的影长为
米,落在地面上的影长为![]() 米,则树高
米,则树高![]() 为多少米.
为多少米.
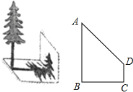
![]() 小明在某一时刻测得
小明在某一时刻测得![]() 的杆子在阳光下的影子长为
的杆子在阳光下的影子长为![]() ,他想测量电线杆
,他想测量电线杆![]() 的高度,但其影子恰好落在土坡的坡面
的高度,但其影子恰好落在土坡的坡面![]() 和地面
和地面![]() 上,量得
上,量得![]() ,
,![]() ,
,![]() 与地面成
与地面成![]() .
.
求电线杆的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AB=12cm,AD=5cm,E是DC上一点(点E不与D、C重合)连接AE,以AE所在的直线为折痕,折叠纸片,点D的对应点为D′,点F为线段BC上一点,连接EF,以EF所在的直线为折痕折叠纸片,使点C的对应点C′落在直线ED′上,若CF=4时,DE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线BC:![]() ,直线BD与x轴交于点A,点B(2,3),点D(0,
,直线BD与x轴交于点A,点B(2,3),点D(0,![]() ).
).
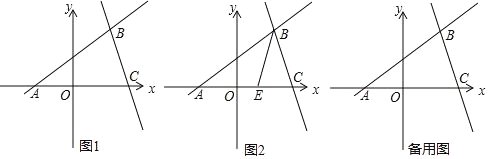
(1)求直线BD的函数解析式;
(2)在y轴上找一点P,使得△ABC与△ACP的面积相等,求出点P的坐标;
(3)如图2,E为线段AC上一点,连结BE,一动点F从点B出发,沿线段BE以每秒1个单位运动到点E再沿线段EA以每秒![]() 个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.
个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其中点
,其中点![]() 的坐标为
的坐标为![]()

![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 若点
若点![]() 在抛物线上,且
在抛物线上,且![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 设点
设点![]() 是线段
是线段![]() 上的动点,作
上的动点,作![]() 轴交抛物线于点
轴交抛物线于点![]() ,求线段
,求线段![]() 长度的最大值.
长度的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com