
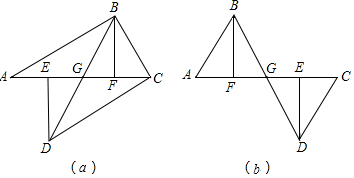
分析 (1)要证明BD平分EF(即EG=FG),可证明EG与FG所在的三角形全等(即证明△EGD≌△FGB),由于DE⊥AC、BF⊥AC,∠BGF与∠DGE是对顶角的条件,所以解决问题的关键是证明有一条边相等(DE=BF),可通过证明△EDC与△FBA全等来实现,说明△EDC≌△FBA,通过AE=CF证明CE=AF是关键;
(2)平移后△EDC与△FBA仍然相似,可仿照(1)进行推理证明.
解答 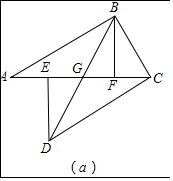 解:(1)∵AE=CF,EF=EF,
解:(1)∵AE=CF,EF=EF,
∴AE+EF=CF+EF,即AF=CE
∵DE⊥AC、BF⊥AC,
∴∠DEG=∠BFG=90°
在Rt△ABF和Rt△CED中,
$\left\{\begin{array}{l}{AF=CE}\\{AB=CD}\end{array}\right.$
∴△ABF≌△CED.
∴ED=BF,
∵在△DEG和△BFG中,
$\left\{\begin{array}{l}{∠EGD=∠BGF}\\{∠DEG=∠BFG}\\{DE=BF}\end{array}\right.$
∴△DEG≌△BFG,
∴EG=FG,即BD平分EF.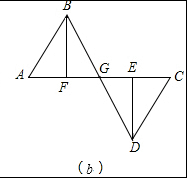
(2)BD仍然平分EF.
理由:∵AE=CF,EF=EF,
∴AE-EF=CF-EF,即AF=CE
∵DE⊥AC、BF⊥AC,
∴∠DEG=∠BFG=90°
在Rt△ABF和Rt△CED中,
$\left\{\begin{array}{l}{AF=CE}\\{AB=CD}\end{array}\right.$
∴△ABF≌△CED.
∴ED=BF,
∵在△DEG和△BFG中,
$\left\{\begin{array}{l}{∠EGD=∠BGF}\\{∠DEG=∠BFG}\\{DE=BF}\end{array}\right.$
∴△DEG≌△BFG,
∴EG=FG,即BD平分EF
点评 本题考查了三角形的判定和三角形的性质.解决本题亦可连接EB、FD,证明四边形BEDF是平行四边形,利用平行四边形的性质说明BD平分EF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.
某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
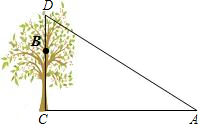 如图,一棵树CD,在其6m高的点B处有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树12m处的池塘A处,另一只猴子爬到树顶D后直线跃向池塘的A处.如果两只猴子所经过的路程相等,试问这棵树有多高?
如图,一棵树CD,在其6m高的点B处有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树12m处的池塘A处,另一只猴子爬到树顶D后直线跃向池塘的A处.如果两只猴子所经过的路程相等,试问这棵树有多高?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com