
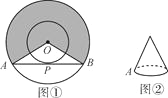
【题目】如图①,两同心圆的圆心为O,大圆的弦AB与小圆相切于点P,已知两圆的半径分别为2和1.
(1)用阴影部分的扇形围成一个圆锥(OA与OB重合),求该圆锥的底面半径.
(2)用余下部分再围成一个圆锥(如图②所示),若一只小虫从A点出发,绕圆锥的侧面爬行一周后又回到A点,求小虫爬行的最短路线的长.
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式为“单人组”和“双人组”.小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于函数![]() 的四个命题:
的四个命题:
①当x=0时,y有最小值6;
② m为任意实数,x=2-m时的函数值大于x=2+m时的函数值;
③若函数图象过点(a,m0) 和(b, m0+1),其中a>0,b>2,则a<b;
④若m>2,且m是整数,当m≤x≤m+1 时,y的整数值有(2m-2)个.
其中真命题有______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
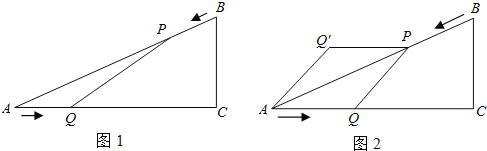
【题目】如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6 cm ,如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm /s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)当t为何值时,PQ∥BC.
(2)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在求出此时t的值;若不存在,请说明理由.
(3)如图2,把△APQ沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k-1)x+k2=0有两个实根x1和x2
(1) 求实数k的取值范围
(2) 若方程两实根x1、x2满足x12-x22=0,求k的值
查看答案和解析>>
科目:初中数学 来源: 题型:
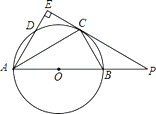
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC、BC.
(1)求证:AC平分∠BAD.
(2)求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,身高1.6米的小明从距路灯的底部(点O)20米的点A沿AO方向行走14米到点C处,小明在A处,头顶B在路灯投影下形成的影子在M处.
(1)已知灯杆垂直于路面,试标出路灯P的位置和小明在C处,头顶D在路灯投影下形成的影子N的位置.
(2)若路灯(点P)距地面8米,小明从A到C时,身影的长度是变长了还是变短了?变长或变短了多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com