Question

已知直角梯形的一条腰与一条对角线相等，且互相垂直，则其上底与下底之比为________．

Answer 1

1：2
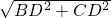
分析：求出BD=DC，根据勾股定理求出BC==BD，求出AD=AB，根据勾股定理求出BD=AD，代入求出即可．
解答：
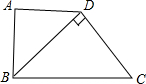
∵BD=CD，BD⊥DC，
∴∠C=∠DBC=45°，
由勾股定理得：BC=BD，
∵∠ABC=90°=∠A，
∴∠ABD=90°-45°=45°，
∴∠ADB=90°-45°=45°=∠ABD，
∴AD=AB，
由勾股定理得：BD=AD，
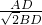
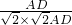
即====1：2，
故答案为：1：2．
点评：本题考查的知识点有等腰三角形的性质和判定，勾股定理，三角形的内角和定理，直角梯形的性质，关键是求出BC=BD，BD=AD，主要考查学生的推理能力．