
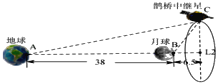
°æƒø°ø2019ƒÍ1‘¬3»’£¨Êœ∂Àƒ∫≈ÃΩ≤‚∆˜◊‘÷˜◊≈¬‰‘⁄‘¬«Ú±≥√Ê£¨ µœ÷»À¿ýÃΩ≤‚∆˜ ◊¥Œ‘¬±≥»Ì◊≈¬Ω£Æµ± ±£¨÷–π˙“—÷«∞∑¢…‰µƒ°∞»µ«≈°±÷–ºÃ–«’˝‘⁄µÿ«Ú°¢‘¬«Ú—”≥§œþ…œµƒL2µ„(µ⁄∂˛¿≠∏Ò¿ »’µ„)∏ΩΩ¸£¨—ÿL2µ„µƒ∂Øè∆Ω∫‚πϵ¿∑…––£¨Œ™Êœ∂Àƒ∫≈◊≈¬Ω∆˜∫Õ‘¬«Ú≥µÃ·π©µÿ«Ú°¢‘¬«Ú÷–ºÃÕ®–≈÷ß≥÷£¨±£’œÊœ∂Àƒ∫≈»ŒŒÒµƒÕÍ≥…”Î µ ©£Æ»ÁÕº£¨“—÷™‘¬«ÚµΩµÿ«Úµƒ∆Ωæ˘æý¿Î‘ºŒ™38ÕÚπ´¿Ô£¨L2µ„µΩ‘¬«Úµƒ∆Ωæ˘æý¿Î‘ºŒ™6.5ÕÚπ´¿Ô£Æƒ≥øã¨≤‚µ√œþ∂ŒCL2”ÎAL2¥π÷±£¨°œCBL2£Ω56°„£¨‘Úœ¬¡–º∆À„»µ«≈÷–ºÃ–«µΩµÿ«Úµƒæý¿ÎAC∑Ω∑®’˝»∑µƒ «( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()

| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡À√¿ªØ≥« –ª∑æ≥£¨ƒ≥Ω÷µ¿÷ÿ–Þ¡À¬∑√Ê£¨◊º±∏Ω´¿œæ…µƒ¬∑µ∆ªª≥…LEDô—كЬ∑µ∆£¨º∆ªÆπ∫¬Ú∫£¬ð±€∫ÕA◊÷±€¡Ω÷÷–Õ∫≈µƒÃ´—كЬ∑µ∆π≤100÷ª£¨æ≠π˝ –≥°µ˜≤È£∫π∫¬Ú∫£¬ð±€Ã´—كЬ∑µ∆1÷ª£¨A◊÷±€Ã´—كЬ∑µ∆2÷ªπ≤–Ë2300‘™£ªπ∫¬Ú∫£¬ð±€Ã´—كЬ∑µ∆3÷ª£¨A◊÷±€Ã´—كЬ∑µ∆4÷ªπ≤–Ë5400‘™£Æ

£®1£©«Û∫£¬ð±€Ã´—كЬ∑µ∆∫ÕA◊÷±€Ã´—كЬ∑µ∆µƒµ•º€£∫
£®2£©‘⁄ µº π∫¬Ú ±£¨«°∑ͅú“ªÓ∂Ø£¨π∫¬Ú∫£¬ð±€Ã´—كЬ∑µ∆≥¨π˝20÷ª ±£¨≥¨π˝µƒ≤ø∑÷¥Úæ≈’€”≈ªð£¨A◊÷±€Ã´—كЬ∑µ∆»´≤ø¥Ú∞À’€”≈ªð£ª»ÙπÊ∂®π∫¬Úµƒ∫£¬ð±€Ã´—كЬ∑µ∆µƒ ˝¡ø≤ª…Ÿ”⁄A◊÷±€Ã´—كЬ∑µ∆µƒ ˝¡øµƒ“ª∞Σ¨«Îƒ„…˺∆“ª÷÷π∫¬Ú∑Ω∞∏£¨ πµ√◊Ð∑—”√◊Ó…Ÿ£¨≤¢«Û≥ˆ◊Ó–°◊Ð∑—”√£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
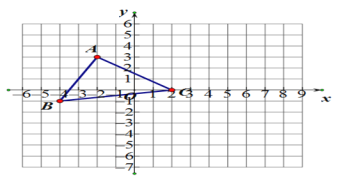
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨°˜ABCµƒ∂•µ„◊¯±Í «A£®©Å2£¨3£©£¨B£®©Å4£¨©Å1£©£¨ C£®2£¨0£©£Æµ„P£®m£¨n£©Œ™°˜ABCƒ⁄“ªµ„£¨∆Ω“∆°˜ABCµ√µΩ°˜A1B1C1 £¨ πµ„P£®m£¨n£©“∆µΩP£®m+6£¨n+1£©¥¶£Æ
£®1£©ª≠≥ˆ°˜A1B1C1
£®2£©Ω´°˜ABC»∆◊¯±Íµ„CƒÊ ±’Ζ˝◊™90°„µ√µΩ°˜A2B2C£¨ª≠≥ˆ°˜A2B2C£ª
£®3£©‘⁄£®2£©µƒÃıº˛œ¬«ÛBC…®π˝µƒ√ʪ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy£Ω©Å![]() x2+bx+c”Îx÷·Ωª”⁄A°¢B¡Ωµ„£¨÷±œþy£Ω
x2+bx+c”Îx÷·Ωª”⁄A°¢B¡Ωµ„£¨÷±œþy£Ω![]() x+
x+![]() æ≠π˝µ„A£¨”Î≈◊ŒÔœþµƒ¡Ì“ª∏ˆΩªµ„Œ™µ„C(3£¨m)£¨œþ∂ŒPQ‘⁄œþ∂ŒAB…œ“∆∂Ø£¨PQ£Ω1£¨∑÷±π˝µ„P°¢Q◊˜x÷·µƒ¥πœþ£¨Ωª≈◊ŒÔœþ”⁄E°¢F£¨Ωª÷±œþ”⁄D°¢G£Æ
æ≠π˝µ„A£¨”Î≈◊ŒÔœþµƒ¡Ì“ª∏ˆΩªµ„Œ™µ„C(3£¨m)£¨œþ∂ŒPQ‘⁄œþ∂ŒAB…œ“∆∂Ø£¨PQ£Ω1£¨∑÷±π˝µ„P°¢Q◊˜x÷·µƒ¥πœþ£¨Ωª≈◊ŒÔœþ”⁄E°¢F£¨Ωª÷±œþ”⁄D°¢G£Æ
(1)«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
(2)…ËÀƒ±þ–ŒDEFGµƒ√ʪ˝Œ™S£¨«ÛSµƒ◊Ó¥Û÷µ£ª
(3)‘⁄œþ∂ŒPQµƒ“∆∂Øπ˝≥Ã÷–£¨“‘D£¨E£¨F£¨GŒ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ ±£¨«Ûµ„Pµƒ◊¯±Í£Æ
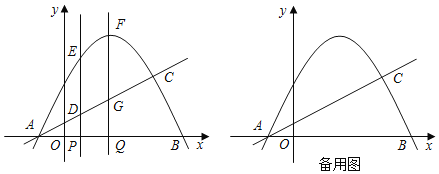
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþ![]() ”Îx÷·Ωª”⁄µ„A£¨B£¨»Ùµ„Bµƒ◊¯±ÍŒ™
”Îx÷·Ωª”⁄µ„A£¨B£¨»Ùµ„Bµƒ◊¯±ÍŒ™![]() .
.
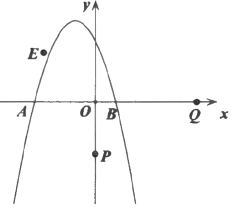
(1)«Û≈◊ŒÔœþµƒΩ‚Œˆ Ωº∞∂•µ„◊¯±Í£ª
(2)»Ù![]() «
«![]() ÷·…œ“ªµ„£¨
÷·…œ“ªµ„£¨![]() £¨Ω´µ„Q»∆◊≈µ„PƒÊ ±’Î∑ΩœÚ–˝◊™90µ√µΩµ„E.
£¨Ω´µ„Q»∆◊≈µ„PƒÊ ±’Î∑ΩœÚ–˝◊™90µ√µΩµ„E.
¢Ÿ”√∫¨tµƒ Ω◊”±Ì 浄![]() µƒ◊¯±Í£ª
µƒ◊¯±Í£ª
¢⁄µ±µ„E«°∫√‘⁄∏√≈◊ŒÔœþ…œ ±£¨«Ûtµƒ÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨’˝∑Ω–ŒABCD÷–£¨AB£Ω5£¨µ„EŒ™BC±þ…œ“ª∂ص„£¨¡¨Ω”AE£¨“‘AEŒ™±þ£¨‘⁄œþ∂ŒAE”“≤ý◊˜’˝∑Ω–Œ![]() £¨¡¨Ω”CF°¢DF£Æ…Ë
£¨¡¨Ω”CF°¢DF£Æ…Ë![]() £Æ(µ±µ„E”ε„B÷ÿ∫œ ±£¨xµƒ÷µŒ™0)£¨
£Æ(µ±µ„E”ε„B÷ÿ∫œ ±£¨xµƒ÷µŒ™0)£¨![]() £Æ–°√˜∏˘æð—ßœ∞∫Ø ˝µƒæ≠—È£¨∂‘∫Ø ˝
£Æ–°√˜∏˘æð—ßœ∞∫Ø ˝µƒæ≠—È£¨∂‘∫Ø ˝![]() ÀÊ◊‘±‰¡øxµƒ±‰ªØ∂¯±‰ªØµƒπʬ…Ω¯––¡ÀÃΩæø£Æœ¬√Ê «–°√˜µƒÃΩæøπ˝≥㨫Î≤π≥‰ÕÍ’˚£∫
ÀÊ◊‘±‰¡øxµƒ±‰ªØ∂¯±‰ªØµƒπʬ…Ω¯––¡ÀÃΩæø£Æœ¬√Ê «–°√˜µƒÃΩæøπ˝≥㨫Î≤π≥‰ÕÍ’˚£∫
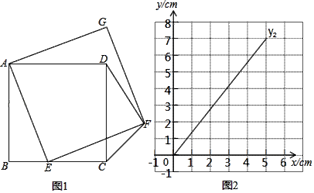
(1)Õ®π˝»°µ„°¢ª≠Õº°¢≤‚¡ø°¢π€≤Ï°¢º∆À„£¨µ√µΩ¡Àx”Îy1°¢y2µƒº∏◊È∂‘”¶÷µ£ª
x | 0 | 1 | 2 | 3 | 4 | 5 |
| 5.00 | 4.12 | 3.61 | 4.12 | 5.00 | |
| 0 | 1.41 | 2.83 | 4.24 | 5.65 | 7.07 |
(2)‘⁄Õ¨“ª∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨√Ë≥ˆ≤π»´∫Ûµƒ±Ì÷–∏˜◊È ˝÷µÀ˘∂‘”¶µƒµ„![]() £¨≤¢ª≠≥ˆ∫Ø ˝y1£¨y2µƒÕºœÛ£ª
£¨≤¢ª≠≥ˆ∫Ø ˝y1£¨y2µƒÕºœÛ£ª
(3)Ω·∫œ∫Ø ˝ÕºœÛ2£¨Ω‚戌 £∫µ±°˜CDFŒ™µ»—¸»˝Ω«–Œ ±£¨BEµƒ≥§∂»‘ºŒ™°° °°cm£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»Ùπÿ”⁄xµƒ∑Ω≥Ã(a+1)x2+(2a©Å3)x+a©Å2£Ω0”–¡Ω∏ˆ≤ªœýµ»µƒ µ∏˘£¨«“πÿ”⁄xµƒ∑Ω≥Ã![]() µƒΩ‚Œ™’˚ ˝£¨‘Ú¬˙◊„Ãıº˛µƒÀ˘”–’˚ ˝aµƒ∫Õ «_____£Æ
µƒΩ‚Œ™’˚ ˝£¨‘Ú¬˙◊„Ãıº˛µƒÀ˘”–’˚ ˝aµƒ∫Õ «_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£Æ‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£Æ≈◊ŒÔœþy£Ω![]() x2+bx+c”Îx÷·Ωª”⁄A¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨µ„Aµƒ◊¯±ÍŒ™£®©Å1£¨0£©£¨µ„Cµƒ◊¯±ÍŒ™£®0£¨©Å2£©£Æ“—÷™µ„E£®m£¨0£© «œþ∂ŒAB…œµƒ∂ص„£®µ„E≤ª”ε„A£¨B÷ÿ∫œ£©£Æπ˝µ„E◊˜PE°Õx÷·Ωª≈◊ŒÔœþ”⁄µ„P£ÆΩªBC”⁄µ„F£Æ
x2+bx+c”Îx÷·Ωª”⁄A¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨µ„Aµƒ◊¯±ÍŒ™£®©Å1£¨0£©£¨µ„Cµƒ◊¯±ÍŒ™£®0£¨©Å2£©£Æ“—÷™µ„E£®m£¨0£© «œþ∂ŒAB…œµƒ∂ص„£®µ„E≤ª”ε„A£¨B÷ÿ∫œ£©£Æπ˝µ„E◊˜PE°Õx÷·Ωª≈◊ŒÔœþ”⁄µ„P£ÆΩªBC”⁄µ„F£Æ
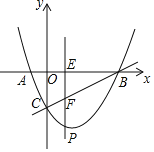
£®1£©«Û∏√≈◊ŒÔœþµƒ±Ì¥Ô Ω£ª
£®2£©µ±œþ∂ŒEF£¨PFµƒ≥§∂»±»Œ™1£∫2 ±£¨«Î«Û≥ˆmµƒ÷µ£ª
£®3£© «∑ҥʑ⁄’‚—˘µƒm£¨ πµ√°˜BEP”ΰ˜ABCœýÀ∆£ø»Ù¥Ê‘⁄£¨«Û≥ˆ¥À ±mµƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨![]() Œ™◊¯±Í‘≠µ„£¨π˝∂˛¥Œ∫Ø ˝
Œ™◊¯±Í‘≠µ„£¨π˝∂˛¥Œ∫Ø ˝![]() ÕºœÛ…œµƒµ„
ÕºœÛ…œµƒµ„![]() £¨◊˜
£¨◊˜![]() ÷·µƒ¥πœþΩª
÷·µƒ¥πœþΩª![]() ÷·”⁄µ„
÷·”⁄µ„![]() .
.
£®1£©»ÁÕº1£¨![]() Œ™œþ∂Œ
Œ™œþ∂Œ![]() …œ∑Ω≈◊ŒÔœþ…œµƒ“ªµ„£¨‘⁄
…œ∑Ω≈◊ŒÔœþ…œµƒ“ªµ„£¨‘⁄![]() ÷·…œ»°µ„
÷·…œ»°µ„![]() £¨µ„
£¨µ„![]() °¢
°¢![]() Œ™
Œ™![]() ÷·…œµƒ¡Ω∏ˆ∂ص„£¨µ„
÷·…œµƒ¡Ω∏ˆ∂ص„£¨µ„![]() ‘⁄µ„
‘⁄µ„![]() µƒ…œ∑Ω«“
µƒ…œ∑Ω«“![]() ¡¨Ω”
¡¨Ω”![]() £¨µ±Àƒ±þ–Œ
£¨µ±Àƒ±þ–Œ![]() µƒ√ʪ˝◊Ó¥Û ±£¨«Û
µƒ√ʪ˝◊Ó¥Û ±£¨«Û![]() µƒ◊Ó–°÷µ.
µƒ◊Ó–°÷µ.
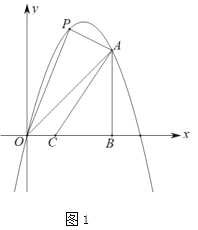
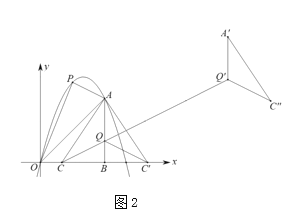
£®2£©»ÁÕº2£¨µ„![]() ‘⁄œþ∂Œ
‘⁄œþ∂Œ![]() …œ£¨¡¨Ω”
…œ£¨¡¨Ω”![]() £¨Ω´
£¨Ω´![]() —ÿ÷±œþ
—ÿ÷±œþ![]() ∑≠’€£¨
∑≠’€£¨![]() µ„µƒ∂‘”¶µ„Œ™
µ„µƒ∂‘”¶µ„Œ™![]() £¨Ω´
£¨Ω´![]() —ÿ…‰œþ
—ÿ…‰œþ![]() ∆Ω“∆
∆Ω“∆![]() ∏ˆµ•Œªµ√
∏ˆµ•Œªµ√![]() £¨‘⁄≈◊ŒÔœþ…œ»°“ªµ„
£¨‘⁄≈◊ŒÔœþ…œ»°“ªµ„![]() £¨ πµ√“‘
£¨ πµ√“‘![]() Œ™∂•µ„µƒ»˝Ω«–Œ «µ»—¸»˝Ω«–Œ£¨«Û
Œ™∂•µ„µƒ»˝Ω«–Œ «µ»—¸»˝Ω«–Œ£¨«Û![]() µ„µƒ◊¯±Í.
µ„µƒ◊¯±Í.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com