
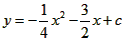 与x轴交于A、B两点(A在B的左边),与y轴交于点C,OC=4。
与x轴交于A、B两点(A在B的左边),与y轴交于点C,OC=4。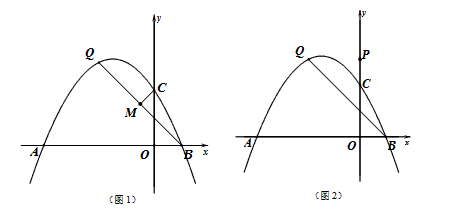
| 解:(1)4; | |
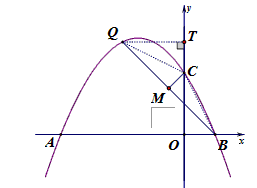
| (2)①连结CQ、BC, 由(1)得:c=4,则抛物线的解析式是 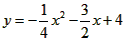 ∵点Q在抛物线上,且横坐标为-4, ∴当x=-4时,y=6, ∴点Q坐标为(-4,6) 连结QC、BC,作QT⊥y轴于点T,如图, 令y=0,则 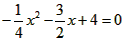 ,解得: ,解得: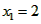 或 或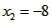 ,则OB=2 ,则OB=2在Rt△BOC中,由勾股定理得: 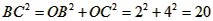 在 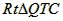 中,由勾股定理得: 中,由勾股定理得: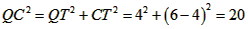 ∴ 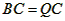 ,即△BCQ是等腰三角形, ,即△BCQ是等腰三角形,又点M为线段BQ的中点, ∴CM⊥BQ; ②存在,理由如下: 设P的坐标为(0,n),在△BPQ中, 若 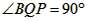 ,由勾股定理得: ,由勾股定理得: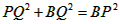 , ,∴ 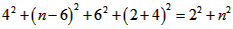 ,解得n=10, ,解得n=10,此时点的坐标为P1(0,10), 若 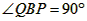 ,由勾股定理得: ,由勾股定理得: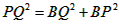 , ,∴ 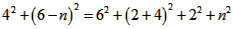 ,解得 ,解得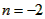 , ,此时点P的坐标为 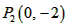 , ,若 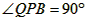 ,由勾股定理得: ,由勾股定理得: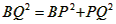 , ,∴ 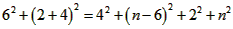 ,解得 ,解得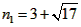 , ,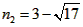 此时点P的坐标为 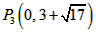 或 或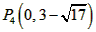 综上,存在这样的点P,使得△BPQ是直角三角形,点P的坐标为: 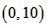 、 、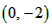 、 、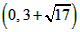 或 或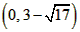 。 。 |
 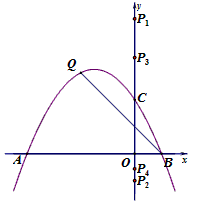 |


科目:初中数学 来源: 题型:
 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.
如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是| 10 |
| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.
如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).
如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com