
已知点P是矩形ABCD边AB上的任意一点(与点A、B不重合)
(1)如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取一点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;
(2)在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由;
(3)如图③,分别在AD、BC上取点F、C’,使得∠APF=∠BPC’,与(1)中的操作相类似,即将△PAF沿PF翻折得到△PFG,并将△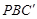 沿
沿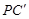 翻折得到△
翻折得到△ ,连接
,连接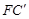 ,取
,取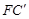 的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.
的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.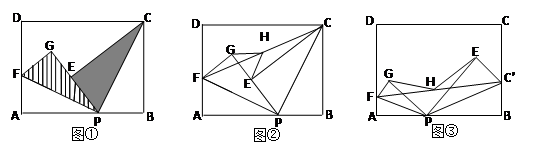
(1)FG∥CE,在矩形ABCD中,∠A=∠B=90°,由题意得,∠G=∠A=90°,∠PEC=∠B=90°,∴∠GEC=90°,∴∠G=∠GEC,∴FG∥CE。
(2)GH=EH。延长GH交CE于点M,由(1)得,FG∥CE,∴∠GFH=∠MCH,∵H为CF的中点,∴FH=CH,又∵∠GHF=∠MHC,∴△GFH≌△MHC,∴GH=HM= ,∵∠GEC=90°,∴EH=
,∵∠GEC=90°,∴EH= ,∴GH=EH。
,∴GH=EH。
(3)(2)中的结论还成立。取PF的中点M,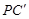 的中点N,∵∠FGP=90°,M为PF的中点,∴
的中点N,∵∠FGP=90°,M为PF的中点,∴ ,
, ,
, ∥
∥ ,∴GM=PM,∴∠GPF=∠MGP,∴∠GMF=∠GPF+∠MGP=2∠GPF,∵H为
,∴GM=PM,∴∠GPF=∠MGP,∴∠GMF=∠GPF+∠MGP=2∠GPF,∵H为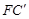 的中点,M为PF的中点,∴
的中点,M为PF的中点,∴ ,同理
,同理 ,
, ,HN∥PF,∠
,HN∥PF,∠ ,∴GM=HN,HM=EN。∵∠GPF=∠FPA,
,∴GM=HN,HM=EN。∵∠GPF=∠FPA, ,又
,又 ,∴∠GPF=
,∴∠GPF= ,∴∠GMF=∠
,∴∠GMF=∠ ,∵
,∵ ∥
∥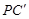 ,HN∥PF,∴四边形HMPN为平行四边形,∴∠HMF=∠
,HN∥PF,∴四边形HMPN为平行四边形,∴∠HMF=∠ ,∴∠GMH=∠HNE,∵GM=HN,HM=EN,∴△GMH≌△HNE,∴GH=HE。
,∴∠GMH=∠HNE,∵GM=HN,HM=EN,∴△GMH≌△HNE,∴GH=HE。
解析


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
 18、如图,已知点D是△ABC的边BC(不含点B,C)上的一点,DE∥AB交AC于点E,DF∥AC交AB于点F、要使四边形AFDE是矩形,则在△ABC中要增加的一个条件是:
18、如图,已知点D是△ABC的边BC(不含点B,C)上的一点,DE∥AB交AC于点E,DF∥AC交AB于点F、要使四边形AFDE是矩形,则在△ABC中要增加的一个条件是:查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
(1)要使四边形AFDE是菱形,则在△ABC中要增加条件__________.
(2)要使四边形AFDE是矩形,则在△ABC中要增加条件__________.
(3)要使四边形AFDE是正方形,则在△ABC中需增加条件___________.
选择一种简述你填写的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知点D是△ABC的边BC(不含点B,C)上的一点,DE∥AB交AC于点E,DF∥AC交AB于点F、要使四边形AFDE是矩形,则在△ABC中要增加的一个条件是:________.
如图,已知点D是△ABC的边BC(不含点B,C)上的一点,DE∥AB交AC于点E,DF∥AC交AB于点F、要使四边形AFDE是矩形,则在△ABC中要增加的一个条件是:________.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:江苏省期末题 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com