
【题目】在直角三角形![]() 中,已知
中,已知![]() ,
,![]() 内有一点
内有一点![]() ,则
,则![]() 的最小值为_______________________。
的最小值为_______________________。
【答案】![]()
【解析】
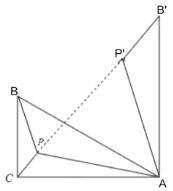
将△APB绕点A顺时针旋转60°至△AP′B′处,连接PP′,根据直角三角形30°角所对的直角边等于斜边的一半求出AB=6,即AB′的长,再根据旋转的性质求出△APP′是等边三角形,利用等边三角形的性质可得AP=PP′,然后可得C、P、P′、B′四点共线时,PA+PB+PC取最小值,再利用勾股定理列式求出CB′即可.
解:如图,将△APB绕点A顺时针旋转60°至△AP′B′处,连接PP′,
∵在Rt△ABC中,∠BCA=90°,BC=3,∠BAC=30°,
∴AB=6,
∴AC=![]() ,
,
∵△APB绕点A顺时针方向旋转60°得到△AP′B′,
∴AP=AP′,∠PAP′=60°,AB′=AB=6,BP=P′B′,∠B′AC=∠BAC+60°=30°+60°=90°,
∴△APP′是等边三角形,
∴AP=PP′,
∴PA+PB+PC=PP′+P′B′+PC,
∴当C、P、P′、B′四点共线时,PA+PB+PC取最小值,
此时PA+PB+PC=PP′+P′B′+PC=CB′=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
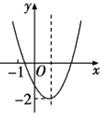
【题目】已知二次函数y=ax2+bx+c(a≠0)的图像如图所示,并且关于x的一元二次方程ax2+bx+c–m=0有两个实数根,下列结论:①b2-4ac>0;②abc>0;③a-b+c>0;④m≥-2,其中正确的个数有( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点![]() ,
,![]() ,
,![]() 三点,点
三点,点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 是线段
是线段![]() 上的一个动点,设点
上的一个动点,设点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
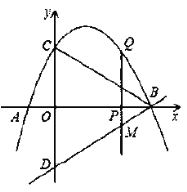
(1)求该抛物线所表示的二次函数的表达式;
(2)在点![]() 运动过程中,是否存在点
运动过程中,是否存在点![]() ,使得以
,使得以![]() 为直径的圆与
为直径的圆与![]() 轴相切?若存在,求出
轴相切?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)连接![]() ,将
,将![]() 绕平面内某点
绕平面内某点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,点
,点![]() 、
、![]() 、
、![]() 的对应点分别是点
的对应点分别是点![]() 、
、![]() 、
、![]() .若
.若![]() 的两个顶点恰好落在抛物线上,那么我们就称这样的点
的两个顶点恰好落在抛物线上,那么我们就称这样的点![]() 为“和谐点”, 那么我们就称这样的点为“和谐点”,请直接写出“和谐点”的个数和点A1的横坐标.
为“和谐点”, 那么我们就称这样的点为“和谐点”,请直接写出“和谐点”的个数和点A1的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息回答下列问题:

(1)求本次测试共调查了多少名学生?
(2)求本次测试结果为B等级的学生数,并补全条形统计图;
(3)若该中学八年级共有900名学生,请你估计八年级学生中体能测试结果为D等级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
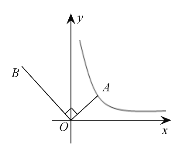
【题目】如图,已知点A是反比例函数 y = ![]() (x>0 )的图象上的一个动点,连接OA ,OB⊥OA,且OB =2OA.那么经过点B的反比例函数的表达式为( )
(x>0 )的图象上的一个动点,连接OA ,OB⊥OA,且OB =2OA.那么经过点B的反比例函数的表达式为( )
A.y=-![]() B.y=
B.y= ![]() C.y=-
C.y=-![]() D.y=
D.y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处![]() 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈![]() ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
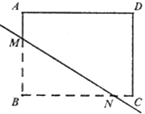
【题目】如图,已知矩形ABCD中,AB=6,AD=8将矩形ABCD沿直线MN翻折后,点B恰好落在边AD上的点E处,如果AE=2AM,那么CN的长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com