
【题目】如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.
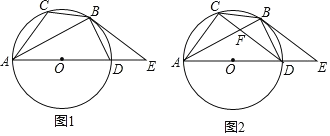
(1)如图1,若BD=![]() ,AC=6
,AC=6
A.求证:BE为圆O的切线
B.求DE的长
(2)如图2,连结CD交AB于点F,若BD=![]() ,CF=3,求圆O的半径.
,CF=3,求圆O的半径.
【答案】(1)A.见解析;B.![]() ;(2)5
;(2)5
【解析】
(1)A.连接OB,由条件可求得∠EBD=∠ABO,再利用圆周角定理可求得∠EBD+∠OBD=90°,可证明BE是⊙O的切线;
B.利用圆内接四边形的性质可求得∠BDE=∠ACB,可证明△ACB∽△BDE,利用相似三角形的性质可求得DE的长;
(2)延长DB、AC交于点H,可证得△ABD≌△ABH,可求得HB,再利用△DCH∽△DBF,可求得DF的长,设⊙O的半径为r,则AD=AH=2r,在Rt△DCH中可求得CH=4,在Rt△ADC中,AD=2r,CD=8,AC=2r-4,由勾股定理可得到关于r的方程,可求得圆的半径.
(1) A.如图1,连接OB,
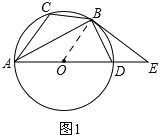
∵BD=BC,
∴∠CAB=∠BAD,
∵∠EBD=∠CAB,
∴∠BAD=∠EBD,
∵AD是⊙O的直径,
∴∠ABD=90°,OA=BO,
∴∠BAD=∠ABO,
∴∠EBD=∠ABO,
∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°,
∵点B在⊙O上,
∴BE是⊙O的切线;
B.∵四边形ACBD是圆的内接四边形,
∴∠ACB=∠BDE,且∠EBD=∠CAB,
∴△ACB∽△BDE,
∴![]() =
=![]() ,即
,即![]() ,
,
解得DE=![]() ;
;
(2)如图2,延长DB、AC交于点H,
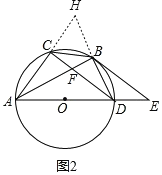
∵AD为⊙O的直径,
∴∠ABD=∠ABH=90°,
∵BD=BC,
∴∠DAB=∠HAB,
在△ABD和△ABH中
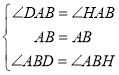
∴△ABD≌△ABH(ASA),
∴BD=HB=![]() ,
,
∵∠DCH=∠FBD=90°,
∴△DCH∽△DBF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得DF=5,
,解得DF=5,
设⊙O的半径为r,则AD=AH=2r,
在Rt△DCH中,CH=![]() =
=![]() =4,
=4,
∴AC=2r4,
在Rt△ACD中,由勾股定理可得AD2=AC2+CD2,
∴(2r)2=(2r4)2+82,解得r=5,
即⊙O的半径为5.


科目:初中数学 来源: 题型:
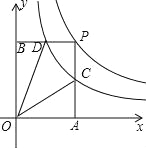
【题目】如图是函数y=![]() 与函数y=
与函数y=![]() 在第一象限内的图象,点P是y=
在第一象限内的图象,点P是y=![]() 的图象上一动点,PA⊥x轴于点A,交y=
的图象上一动点,PA⊥x轴于点A,交y=![]() 的图象于点C,PB⊥y轴于点B,交y=
的图象于点C,PB⊥y轴于点B,交y=![]() 的图象于点D.
的图象于点D.
(1)求证:D是BP的中点;
(2)求四边形ODPC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB=AC,延长BC至点D,使CD=CA,连接AD交⊙O与点E,连接BE,CE.
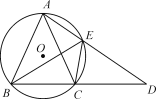
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为______时,四边形AOCE是菱形;
②若AE=![]() ,AB=2
,AB=2![]() ,则DE的长为______.
,则DE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
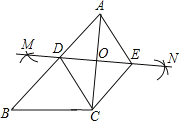
【题目】如图,已知△ABC,按如下步骤作图:
①分别以A、C为圆心,以大于![]() AC的长为半径在AC两边作弧,交于两点M,N;
AC的长为半径在AC两边作弧,交于两点M,N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
(1)求证:四边形ADCE是菱形.
(2)当∠ACB=90°,AC=16,△ADC的周长为36时,直接写出四边形ADCE的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋中装有四个完全相同的小球,它们分别写有“美”“丽”、“椒”、“江”的文字.
(1)先从袋摸出1个球后放回,混合均匀后再摸出1个球,求两次摸出的球上是写有“美丽”二字的概率;
(2)先从袋中摸出1个球后不放回,再摸出1个球。求两次摸出的球上写有“椒江”二字的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备在校园内修建一个矩形的绿化带,矩形的面积为定值,它的一边长![]() 与另一边长
与另一边长![]() 之间的函数图像如图.
之间的函数图像如图.

(1)该绿化带的面积是多少?写出![]() 与
与![]() 的函数解析式.
的函数解析式.
(2)完成下表,并回答问题:如果该绿化带的长![]() 不得超过
不得超过![]() ,那么
,那么![]() 应控制在什么范围?
应控制在什么范围?
| 10 | 20 | 30 | 40 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阳阳超市以每件10元的价格购进了一批玩具,定价为20元时,平均每天可售出80个.经调查发现,玩具的单价每降1元,每天可多售出40个;玩具的单价每涨1元,每天要少售出5个.如何定价才能使每天的利润最大?求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
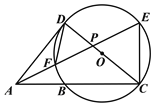
【题目】如图,△ACE,△ACD均为直角三角形,∠ACE=90°,∠ADC=90°,AE与CD相交于点P,以CD为直径的⊙O恰好经过点E,并与AC,AE分别交于点B和点F.
(1)求证:∠ADF=∠EAC.
(2)若PC=![]() PA,PF=1,求AF的长.
PA,PF=1,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 与
与![]() 都是等腰直角三角形,且
都是等腰直角三角形,且![]() ,
,![]() ,连接DC,点M、P、N分别为DE、DC、BC的中点
,连接DC,点M、P、N分别为DE、DC、BC的中点
(1)如图1,当点D、E分别在边AB、AC上,线段PM与PN的数量关系是______,位置关系是______;
(2)把等腰![]() 绕点A旋转到如图2的位置,连接MN,判断
绕点A旋转到如图2的位置,连接MN,判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)把等腰![]() 绕点A在平面内任意旋转,
绕点A在平面内任意旋转,![]() ,
,![]() ,请直接写出
,请直接写出![]() 的面积S的变化范围.
的面积S的变化范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com